题目内容
【题目】如图，点
在双曲线上，
垂直
轴，垂足为
，点
在上，
平行于轴交曲线于点
，直线
与
轴交于点
，已知
，点的坐标为
.
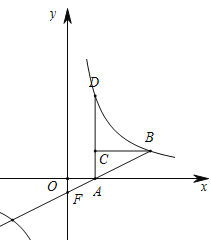
（1）求该双曲线的解析式；
（2）求
的面积.
【答案】（1）双曲线解析式为
；（2）
【解析】
（1）由题意可知点
的坐标为
得
，而
，得到
，则
点坐标为
，然后利用待定系数法确定双曲线的解析式；
（2）根据题意已知
和
，利用待定系数法确定直线
的解析式，得到
点的坐标，然后利用三角形的面积公式进行计算即可．
解：（1）∵点的坐标为，
垂直
轴，
∴，
又∵，
∴，
∴点坐标为，
设双曲线的解析式为
，
把
代入得，
，
所以双曲线解析式为；
（2）设直线的解析式为
，
∵
平行于轴交曲线于点
，
∵双曲线的解析式为，
∴
∴把和代入得
，
，
解得
，
，
∴线段的解析式为
，
令
，得
，
∴点的坐标为
，
∴
．
练习册系列答案
三点一测快乐周计划系列答案
相关题目
