题目内容
12．已知二次函数y=x2+x+2与一次函数y=2x-1在同一坐标系中的交点个数是（ ）| A． | 0个 | B． | 1个 | C． | 2个 | D． | 无法确定 |
分析 根据题意得到方程x2+x+2=2x-1，判断方程根的个数即可作出正确选择．
解答 解：根据题意联立方程可得$\left\{\begin{array}{l}{y={x}^{2}+x+2}\\{y=2x-1}\end{array}\right.$，
即x2+x+2=2x-1，
整理得x2-x+3=0，
△=1-12=-11＜0，
则二次函数y=x2+x+2与一次函数y=2x-1没有交点，
故选A．
点评 本题主要考查了二次函数的性质的知识，解答本题的关键是根据题意可得一元二次方程，进而判断方程根的个数，此题难度不大．
练习册系列答案
相关题目
3．
如图，在△ABC中，∠A=90°，AB=3，BC=5，则cosB等于（ ）
如图，在△ABC中，∠A=90°，AB=3，BC=5，则cosB等于（ ）| A． | $\frac{3}{5}$ | B． | $\frac{4}{5}$ | C． | $\frac{4}{3}$ | D． | $\frac{3}{4}$ |
20．已知a+b=3，ab=2，计算：a2b+ab2等于（ ）
| A． | 5 | B． | 6 | C． | 9 | D． | 1 |
7．下列计算，正确的是（ ）
| A． | 3x2+2x2=6x2 | B． | x3•x2=x6 | C． | x3÷x2=x | D． | （2x2）3=6x6 |
17．下列运算中，结果正确的是（ ）
| A． | x3•x3=x9 | B． | 3x2+2x2=5x2 | C． | x6÷x2=x3 | D． | （x+y）2=x2+y2 |
4．一家广告公司想招聘一名策划部经理，对甲、乙两名应聘应试者进行面试、文案策划、已有经历三项考评，他们的各项成绩（百分制）如下表
（1）如果这家公司想招聘一名综合能力较强的部门经理，计算两名应试者的平均成绩（百分制），从他们成绩看，应录取谁？
（2）如果这家公司想招聘一名综合能力较强的部门经理，面试、文案策划、已有成绩按照4：3：3的比确定，计算两名应试者的平均成绩（百分制），从他们成绩看，应录取谁？
| 应聘者 | 面试 | 文案策划 | 已有经历 |
| 甲 | 88 | 78 | 80 |
| 乙 | 80 | 85 | 83 |
（2）如果这家公司想招聘一名综合能力较强的部门经理，面试、文案策划、已有成绩按照4：3：3的比确定，计算两名应试者的平均成绩（百分制），从他们成绩看，应录取谁？
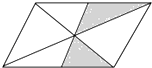如图所示，平行四边形的两条对角线及过对角线交点的任意一条直线将平行四边形纸片分割成六个部分，现在平行四边形纸片上作随机扎针实验，针头扎在阴影区域内的概率为$\frac{1}{4}$．