Question

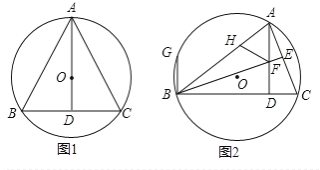
【题目】如图，⊙O中，＝，∠ABC＝75°，BC＝2，则图中阴影部分的面积是（ ）.

A.2＋B.2＋C.4＋D.＋

Answer 1

【答案】A

【解析】

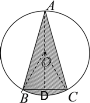
根据圆的基本性质可得：AB=AC，从而得出：点A在BC的中垂线上，∠ABC=∠ACB=75°，根据三角形内角和定理，可求出∠BAC，根据圆周角定理可求出∠BOC,从而判定△OBC是等边三角形，同时可证:AD垂直平分BC,从而求出∠BOD，求出AD，然后利用S阴影=S△ABC＋S扇形OBC－S△OBC即可求出阴影面积.

解：连接AO并延长交BC于D，连接OB、OC，如下图所示

∵＝

∴AB=AC

∴点A在BC的中垂线上，∠ABC=∠ACB=75°

∴∠BAC=180°－∠ABC－∠ACB=30°

∴∠BOC=60°

∵OB=OC

∴△OBC是等边三角形，点O在BC的中垂线上

∴OB=OC=BC=2，AD垂直平分BC

∴OA=OB=2，OD平分∠BOC

∴∠BOD=∠BOC=30°

∴OD=OB·cos∠BOD=

∴AD=AO＋OD=2＋

∴S阴影=S△ABC＋S扇形OBC－S△OBC

=AD·BC＋－OD·BC

=×（2＋）×2＋－××2

=2＋

故选A.