题目内容
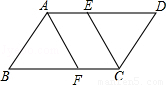
已知E、F分别是平行四边形ABCD的边AB、CD的中点,BD是对角线,AG∥BD交CB的延长线于G. (8分)

1.(1)试说明△ADE≌△CBF;
2.(2)当四边形AGBD是矩形时,请你确定四边形BEDF的形状并说明;
3.(3)当四边形AGBD是矩形时,四边形AGCD是等腰梯形吗?直接说出结论.
1.(1)在 ABCD中,BC=AD,∠C=∠BAD,CD=AB(1分)
∵E、F是AB、CD的中点,∴AE=CF. (2分)
在△BCF、△DAE中,
BC=AD,∠C=∠BAD,AE=CF
∴△ADE≌△CBF (3分)
2.(2)∵BE=DF,BE//DF
∴四边形BEDF为平行四边形 (5分)
当四边形AGBD为矩形时,∠ADB=90°
∴DE=![]() AB=BE (6分)
AB=BE (6分)
 ∴ BEDF为菱形 (7分)
∴ BEDF为菱形 (7分)
3.(3)不可能是等腰梯形(8分) 因为在Rt△DBC中,CD不可能等于BD
解析:略

练习册系列答案
相关题目
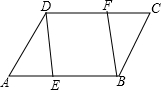 (2013•番禺区一模)如图,已知E、F分别是平行四边形ABCD的边AB、CD上的两点,且∠CBF=∠ADE.
(2013•番禺区一模)如图,已知E、F分别是平行四边形ABCD的边AB、CD上的两点,且∠CBF=∠ADE. 已知E、F分别是平行四边形ABCD的边AB、CD的中点,BD是对角线,AG∥BD交CB的延长线于G.
已知E、F分别是平行四边形ABCD的边AB、CD的中点,BD是对角线,AG∥BD交CB的延长线于G. 如图,已知E,F分别是平行四边形ABCD的边AD、BC上的点,且AE=
如图,已知E,F分别是平行四边形ABCD的边AD、BC上的点,且AE= AD,CF=
AD,CF=