题目内容
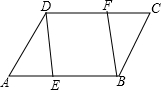 (2013•番禺区一模)如图,已知E、F分别是平行四边形ABCD的边AB、CD上的两点,且∠CBF=∠ADE.
(2013•番禺区一模)如图,已知E、F分别是平行四边形ABCD的边AB、CD上的两点,且∠CBF=∠ADE.(1)求证:△ADE≌△CBF;
(2)判定四边形DEBF是否是平行四边形?
分析:(1)利用平行四边形ABCD的对角相等,对边相等的性质推知∠A=∠C,AD=BC;然后根据全等三角形的判定定理AAS证得结论;
(2)由“对边平行且相等的四边形是平行四边形”推知四边形DEBF是平行四边形.
(2)由“对边平行且相等的四边形是平行四边形”推知四边形DEBF是平行四边形.
解答: (1)证明:∵四边形ABCD为平行四边形,
(1)证明:∵四边形ABCD为平行四边形,
∴∠A=∠C,AD=BC,
在△ADE与△CBF中,
,
∴△ADE≌△CBF(ASA);
(2)解:四边形DEBF是平行四边形.理由如下:
∵DF∥EB,又由△ADE≌△CBF,知AE=CF,
∴AB-AE=CD-CF,即DF=EB.
∴四边形DEBF是平行四边形.
 (1)证明:∵四边形ABCD为平行四边形,
(1)证明:∵四边形ABCD为平行四边形,∴∠A=∠C,AD=BC,
在△ADE与△CBF中,
|
∴△ADE≌△CBF(ASA);
(2)解:四边形DEBF是平行四边形.理由如下:
∵DF∥EB,又由△ADE≌△CBF,知AE=CF,
∴AB-AE=CD-CF,即DF=EB.
∴四边形DEBF是平行四边形.
点评:本题考查了全等三角形的判定与性质、平行四边形的判定与性质.平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
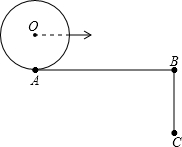 (2013•番禺区一模)如图,已知∠ABC=90°,AB=πr,AB=2BC,半径为r的⊙O从点A出发,沿A→B→C方向滚动到点C时停止.则在此运动过程中,圆心O运动的总路程为( )
(2013•番禺区一模)如图,已知∠ABC=90°,AB=πr,AB=2BC,半径为r的⊙O从点A出发,沿A→B→C方向滚动到点C时停止.则在此运动过程中,圆心O运动的总路程为( ) (2013•番禺区一模)为了提高城市居民的节水意识,有关部门就有效的节水措施随机对部分市民进行了问卷调查.其中调查问卷设置以下选项(被调查者只能选择其中的一项:A.出台相关法律法规;B.控制用水大户数量;C.推广节水技改和节水器具;D.用水量越多,水价越高;E.其他根据调查结果制作了统计图表(不完整)如下:
(2013•番禺区一模)为了提高城市居民的节水意识,有关部门就有效的节水措施随机对部分市民进行了问卷调查.其中调查问卷设置以下选项(被调查者只能选择其中的一项:A.出台相关法律法规;B.控制用水大户数量;C.推广节水技改和节水器具;D.用水量越多,水价越高;E.其他根据调查结果制作了统计图表(不完整)如下: