题目内容
4. 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点P从点A往点B方向运动,速度为2,点Q从点B往点C方向运动,速度为1,设运动时间为t.
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点P从点A往点B方向运动,速度为2,点Q从点B往点C方向运动,速度为1,设运动时间为t.(1)t取何值时以B,P,Q为顶点的三角形为直角三角形;
(2)t取何值时△BPQ面积为△ABC面积的一半.
分析 (1)先利用勾股定理求得BA的长,然后利用相似三角形的性质列出方程求解即可;
(2)根据三角形的面积公式列方程求解即可.
解答 解:(1)∵在Rt△ABC中,∠C=90°,
∴AB=$\sqrt{A{C}^{2}+C{B}^{2}}$=10.
当∠PQB=90°时,
∵∠PQB=∠C=90°,∠B=∠B,
∴△ACB∽△PQB.
∴$\frac{PB}{AB}=\frac{BQ}{BC}$,即$\frac{10-2t}{10}=\frac{t}{8}$.
解得:t=$\frac{40}{13}$.
当∠QPB=90°时,
∵∠QPB=∠C=90°,∠B=∠B,
∴△ACB∽△QPB.
∴$\frac{PB}{BC}=\frac{BQ}{AB}$,即$\frac{10-2t}{8}=\frac{t}{10}$.
解得:t=$\frac{25}{7}$.
答:t=$\frac{40}{13}$s或t=$\frac{25}{7}$s时,△BPQ为直角三角形.
(2)如图所示:过点P作PD⊥BC,垂足为D.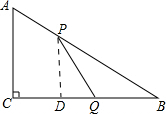
∵∠C=∠PDB=90°,∠B=∠B,
∴△BDP∽△BCA.
∴$\frac{PB}{AB}=\frac{PD}{AC}$,即$\frac{10-2t}{10}=\frac{PD}{6}$.
∴PD=6-$\frac{6}{5}t$.
由三角形的面积公式得:$\frac{1}{2}t•(6-\frac{6}{5}t)=\frac{1}{2}×6×8$×$\frac{1}{2}$,
整理得:t2-5t+10=0,
∵△=(-5)2-4×1×10=-15<0,
∴方程无解.
∴不存在时间t使的△BPQ的面积为△ACB面积的一半.
点评 本题主要考查的是一元二次方程的应用,根据题意列出关于x的方程是解题的关键.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
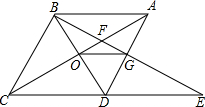 如图,菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连结BE分别交AC,AD于点F、G,连结OG,则下列结论:
如图,菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连结BE分别交AC,AD于点F、G,连结OG,则下列结论: 如图,△ABC中,D为AB边上一点,已知AB=AC,AD=CD=BC,求△ABC中的各角的度数.
如图,△ABC中,D为AB边上一点,已知AB=AC,AD=CD=BC,求△ABC中的各角的度数.
 在方格纸中,每个小方格的顶点称为格点,以格点连线为边的三角形叫做格点三角形.在如图所示的5×5方格中,已知点A(0,-2),B(-1,0),作格点△ABC,使它和△OAB相似(相似比不为1),求点C的坐标.
在方格纸中,每个小方格的顶点称为格点,以格点连线为边的三角形叫做格点三角形.在如图所示的5×5方格中,已知点A(0,-2),B(-1,0),作格点△ABC,使它和△OAB相似(相似比不为1),求点C的坐标. 如图:
如图: