题目内容
如图，已知∠ACB=∠CBD=90°，且BD=a，BC=b，当AC与a，b满足什么关系时，△ACB∽△CBD？
解：∵△ACB∽△CBD，
∴
=
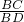
∴AC=
=
，
故当AC=时△ACB∽△CBD．
分析：当△ACB∽△CBD时，根据对应边比值相等的性质，即可求得=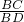，即可求得AC、a、b的关系，即可解题．
点评：本题考查了相似三角形对应边比值相等的性质，考查了相似三角形的判定，本题中根据对应边比值相等的性质求AC、a、b的关系是解题的关键．
∴
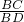
=∴AC=
=，故当AC=
时△ACB∽△CBD．分析：当△ACB∽△CBD时，根据对应边比值相等的性质，即可求得
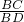=，即可求得AC、a、b的关系，即可解题．点评：本题考查了相似三角形对应边比值相等的性质，考查了相似三角形的判定，本题中根据对应边比值相等的性质求AC、a、b的关系是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，已知∠ACB=∠CBD=90°，BC=a，AC=b，当CD=（ ）时，△CDB∽△ABC．A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，已知∠ACB=∠BDA=90°，要使△ABC≌△BAD，还需要添加一个条件，这个条件可以是
如图，已知∠ACB=90°，∠DAB=70°，AC平分∠DAB，∠1=35°．