题目内容
3. 如图,已知等边△ABC和等边△CDE.求证:BE=AD.
如图,已知等边△ABC和等边△CDE.求证:BE=AD.
分析 易证∠ACD=∠BCE,即可证明△ACD≌△BCE,根据全等三角形对应边相等的性质即可解题.
解答 证明:∵∠ACB=∠DCE,∠ACD+∠BCD=∠ACB,∠BCE+∠BCD=∠DCE,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{DC=CE}\end{array}\right.$,
∴△ACD≌△BCE(SAS),
∴AD=BE.
点评 本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ACD≌△BCE是解题的关键.

练习册系列答案
相关题目
11. 如图是一个指示标志,它的左视图是( )
如图是一个指示标志,它的左视图是( )
 如图是一个指示标志,它的左视图是( )
如图是一个指示标志,它的左视图是( )| A. |  | B. |  | C. |  | D. |  |
15.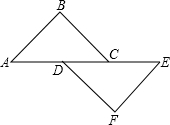 如图,△ABC≌△EFD且AB=EF,CE=2.5,CD=2,则AC=( )
如图,△ABC≌△EFD且AB=EF,CE=2.5,CD=2,则AC=( )
 如图,△ABC≌△EFD且AB=EF,CE=2.5,CD=2,则AC=( )
如图,△ABC≌△EFD且AB=EF,CE=2.5,CD=2,则AC=( )| A. | 2 | B. | 2.5 | C. | 4 | D. | 4.5 |
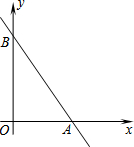 如图,在平面直角坐标系中,直线AB分别交x轴、y轴于A、B两点.
如图,在平面直角坐标系中,直线AB分别交x轴、y轴于A、B两点.
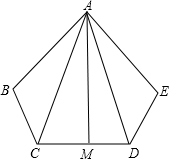 如图,AB=AE,BC=DE,∠B=∠E,AM⊥CD,垂足为M,求证:CM=MD.
如图,AB=AE,BC=DE,∠B=∠E,AM⊥CD,垂足为M,求证:CM=MD.