题目内容
已知:等腰△ABC的顶角∠BAC=120°,腰长AB=5cm,AD为BC边上的中线.求AD的长.
考点:含30度角的直角三角形
专题:
分析:先求出底角等于30°,再根据30°的直角三角形的性质求解即可.
解答:解:∵∠BAC=120°,AB=AC,
∴∠B=∠C=
(180°-120°)=30°.
∵AD为BC边上的中线,
∴AD⊥BC,
∠B=
(180°-120°)=30°.
∴AD=
AB=
×5=
(cm).

∴∠B=∠C=
| 1 |
| 2 |
∵AD为BC边上的中线,
∴AD⊥BC,
∠B=
| 1 |
| 2 |
∴AD=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
点评:本题考查了等腰三角形的三线合一性质和含30°角的直角三角形的性质,关键是根据题意画出图形,找出含30°角的直角三角形.

练习册系列答案
相关题目
直线y=kx+b与y=2x平行,和y轴交于点(0,3),则该函数关系式是( )
| A、y=2x-3 |
| B、y=3x+2 |
| C、y=2x+3 |
| D、y=3x-2 |
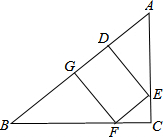 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,在线段AB上取一点D,过D作DE⊥AB交AC于E,过E作EF⊥DE交BC于F,过F作FG⊥EF交AB于G,得到矩形DEFG.
如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,在线段AB上取一点D,过D作DE⊥AB交AC于E,过E作EF⊥DE交BC于F,过F作FG⊥EF交AB于G,得到矩形DEFG. 如图,已知Rt△ABC中,∠C=90°,AB=10cm,AC=8cm.如果点P由B出发沿BA方向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s.连接PQ,设运动的时间为t(单位:s)(0<t≤4).解答下列问题:
如图,已知Rt△ABC中,∠C=90°,AB=10cm,AC=8cm.如果点P由B出发沿BA方向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s.连接PQ,设运动的时间为t(单位:s)(0<t≤4).解答下列问题: 如图,直线AB与x轴、y轴分别相交于A、B点,将直线AB绕点O顺时针旋转90°得到直线A1B1,A、B点的对应点分别是A1、B1.
如图,直线AB与x轴、y轴分别相交于A、B点,将直线AB绕点O顺时针旋转90°得到直线A1B1,A、B点的对应点分别是A1、B1.