题目内容
已知:如图,E为正方形ABCD的边BC延长线上的点,F是CD边上一点,且CE=CF,连接DE、BF.

(1)求证:DE=BF;
(2)判断BF与DE的位置关系,并说明理由.
【答案】
证明见解析.
【解析】
试题分析:根据已知利用边角边得出△ABF≌△CBE,进而求出∠ECB+∠CFH=90°即可.
试题解析:(1)∵正方形ABCD,
∴AB=CB,∠ABC=∠CBE=90°,
∵BE=BF,
 ,
,
∴△ABF≌△CBE (SAS),
∴AF=CE,
(2)延长AF交CE于点H.

∵△ABF≌△CBE
∴∠FAB=∠ECB,
∵∠FAB+∠AFB=90°,
又∵∠AFB=∠CFH,
∴∠ECB+∠CFH=90°,
∴∠CHF=90°,
∴AF⊥CE.
考点:全等三角形的判定与性质.

练习册系列答案
相关题目
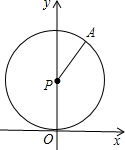 已知:如图,⊙P与x轴切于点O,点P的坐标为(0,1),点A在⊙P上,且在第一象限,∠APO=150°,⊙P沿x轴正方向滚动,当点A第一次落在x轴上时,点P的坐标为
已知:如图,⊙P与x轴切于点O,点P的坐标为(0,1),点A在⊙P上,且在第一象限,∠APO=150°,⊙P沿x轴正方向滚动,当点A第一次落在x轴上时,点P的坐标为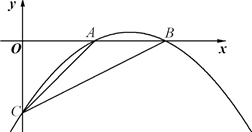 已知:如图,抛物线y=ax2+bx-2交x轴于A,B两点,交y轴于点C,OC=OA,△ABC的面积为2.
已知:如图,抛物线y=ax2+bx-2交x轴于A,B两点,交y轴于点C,OC=OA,△ABC的面积为2. 已知:如图,一次函数y=
已知:如图,一次函数y= 已知:如图所示,直线l的解析式为
已知:如图所示,直线l的解析式为