题目内容
如图,AB是⊙O的直径,且AB=10,直线CD交⊙O于C、D两点,交AB于E,OP⊥CD于P,∠PEO=45°,OP=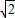 .
.(1)求线段CD的长;
(2)试问将直线CD通过怎样的变换才能与⊙O切于B或A.
【答案】分析:(1)连接OC,得到Rt△CPO,利用勾股定理可以求出CP的长,也就是CD的一半;
(2)先变换成与AB垂直,再进行上下移动使之与圆相切.
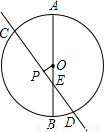
解答: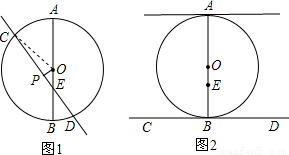 解:(1)如图1,连接OC,
解:(1)如图1,连接OC,
∵OP⊥CD,
∴CP= CD=
CD=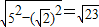 ,
,
∴CD=2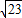 ;(6分)
;(6分)
(2)∵∠PEO=45°,OP=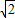 ,
,
∴OE=2,BE=3,
∴将直线CD绕着点E逆时针旋转45°后,若再沿射线EB平移3个单位,直线CD与⊙O相切于B,或再沿射线EA平移7个单位,直线CD与⊙O相切于A(如图2). (12分)
点评:本题主要考查了垂径定理,构造直角三角形,然后利用勾股定理求解是解决本题的关键.
(2)先变换成与AB垂直,再进行上下移动使之与圆相切.
解答:
 解:(1)如图1,连接OC,
解:(1)如图1,连接OC,∵OP⊥CD,
∴CP=
 CD=
CD=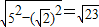 ,
,∴CD=2
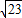 ;(6分)
;(6分)(2)∵∠PEO=45°,OP=
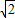 ,
,∴OE=2,BE=3,
∴将直线CD绕着点E逆时针旋转45°后,若再沿射线EB平移3个单位,直线CD与⊙O相切于B,或再沿射线EA平移7个单位,直线CD与⊙O相切于A(如图2). (12分)
点评:本题主要考查了垂径定理,构造直角三角形,然后利用勾股定理求解是解决本题的关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
 8、如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为( )
8、如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为( ) 0.1平方米)
0.1平方米)

 如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为
如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为