题目内容
如图，平行四边形ABCD中，P为边AD的中点，连接PC，若△APC、△PDC、△BAC的面积分别为S、S1、S2，当S=12时，S1+S2=考点：平行四边形的性质
专题：
分析：利用中线的性质得出S△APC=S△CDP，进而得出S1=12，S2=24，即可得出答案．
解答：解：∵P为边AD的中点，
∴S△APC=S△CDP=
S△ADC=12，
∵平行四边形ABCD中，AC是对角线，
∴S△ABC=S△ADC=24，
∴S1=12，S2=24，
∴S1+S2=36．
故答案为：36．
∴S△APC=S△CDP=
| 1 |
| 2 |
∵平行四边形ABCD中，AC是对角线，
∴S△ABC=S△ADC=24，
∴S1=12，S2=24，
∴S1+S2=36．
故答案为：36．
点评：此题主要考查了平行四边形的性质以及三角形中线的性质，得出S△APC=S△CDP是解题关键．
练习册系列答案
相关题目
如图，直线y=-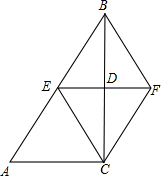
如图，在△ABC中，∠ACB=90°，BC的垂直平分线EF交BC于点D，交AB于点E，且BE=BF，添加一个条件，能证明四边形BECF为正方形的是已知
是二元一次方程组
的解，则a+b的值是（ ）
|
|
| A、1 | B、2 | C、3 | D、-1 |