题目内容
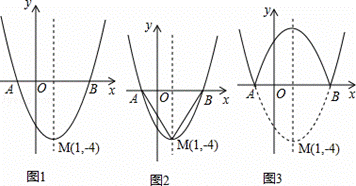
如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,﹣4).
(1)求出图象与x轴的交点A,B的坐标;
(2)在二次函数的图象上是否存在点P,使S△PAB= S△MAB?若存在,求出P点的坐标,若不存在,请说明理由;
S△MAB?若存在,求出P点的坐标,若不存在,请说明理由;
(3)点C在x轴上一动点,以BC为边作正方形BCDE,正方形BCDE还有一个顶点(除点B外)在抛物线上,请写出满足条件的点E的坐标;
(4)将二次函数的图象在x轴下方的部分沿x轴翻折,图象 的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线y=x+b与此图象至少有三个公共点时,请直接写出b的取值范围是 .
的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线y=x+b与此图象至少有三个公共点时,请直接写出b的取值范围是 .
解:(1)∵M(1,﹣4)是二次函数y=(x+m)2+k的顶点坐标,
∴y=(x﹣1)2﹣4=x2﹣2x﹣3,
当 x2﹣2x﹣3=0,解得x1=﹣1,x2=3.
x2﹣2x﹣3=0,解得x1=﹣1,x2=3.
∴A、B两点的坐标 分别为A(﹣1,0),B(3,0);
分别为A(﹣1,0),B(3,0);
(2)在二次函数的图象上存在点P,使
设p(x,y),则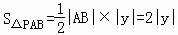 ,又
,又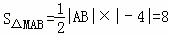 ,
,
∴2|y|=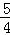 ×8,即y=±5, ∵二次函数的最小值为﹣4, ∴y=5.
×8,即y=±5, ∵二次函数的最小值为﹣4, ∴y=5.
当y=5时,x=﹣2或x=4. ∴P点坐标为(﹣2,5)或(4,5);
(3)不妨设点E在抛物线y=x2﹣ 2x﹣3上,C点的坐标为(m,0).
2x﹣3上,C点的坐标为(m,0).
当BC为正方形BCDE的边时,则E点的坐标为(m,m2﹣2m﹣3).
∵四边形BCDE是正方形,
∴BC=DE, ∴|m﹣3|=|m2﹣2m﹣3|, 即m﹣3=m2﹣2m﹣3,或m﹣3=﹣(m2 ﹣2m﹣3),
﹣2m﹣3),
解得m1=0,m2=3,或m1=﹣2,m2=3,
当m=3时,C点与B点重合,不合题意,舍去,
∴E点的坐标为(0,0)或(﹣2,0),则B1(3,4),B2(3,﹣4),
(4)如图3,依题意知,当﹣1≤x≤3时,翻折后的抛物线的解析式为:y=﹣x2+2x+3
与直线y=x+b与新抛物线有1个交点时,﹣x2+2x+3=x+b,即x2﹣x﹣3﹣b=0,
则△=(﹣1)2﹣4×(﹣3﹣b)=0, 解得 b=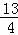
当直线y=x+b经过A(﹣1,0)时﹣1+b=0,可得b=1,
由题意可知y=x+b在y=x+1的下方.由图可知符合题意的b的取值范围1≤b≤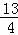 .
.

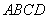 的边长为6厘米,
的边长为6厘米, .从初始时刻开始,点
.从初始时刻开始,点 、
、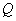 同时从
同时从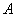 点出发,点
点出发,点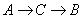 的方向运动,点
的方向运动,点 的方向运动,当点
的方向运动,当点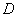 点时,
点时,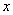 秒时,
秒时,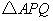 与
与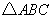 重叠部分的面积为
重叠部分的面积为 平方厘米(这里规定:点和线段是面积为0的三角形),解答下列问题:
平方厘米(这里规定:点和线段是面积为0的三角形),解答下列问题: 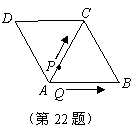 (2)点
(2)点 的值是 秒;
的值是 秒; 3)当0≤
3)当0≤
 的值是在……………………………………………………………【 】
的值是在……………………………………………………………【 】 的立方根是 .
的立方根是 .
