题目内容
如图,在高楼AB前D点测得楼顶A的仰角为30°,向高楼前进60米到C点,又测得楼顶A的仰角为60°,则该高楼AB的高度为 米.


30
 【考点】解直角三角形的应用-仰角俯角问题.
【考点】解直角三角形的应用-仰角俯角问题.
【专题】应用题;推理填空题.
【分析】设AB的长度为x,在Rt△ABC中利用三角函数可以用x表示BC的长度,同理也可以表示BD的长度,而CD=BD﹣BC,然后根据已知条件即可求出x,也就求出了相等AB的长度.
【解答】解:设AB的长度为x,
在Rt△ABC中,tan∠ACB=
 =tan60°=
=tan60°=
 ,
,
∴BC=
 ,
,
同理在Rt△ABD中,BD=
 =
=
 =
=
 x,
x,
而CD=BD﹣BC=60,
∴60=
 x﹣
x﹣
 ,
,
∴x=30
 ,
,
即AB=30
 米.
米.
故答案为:30
 .
.
【点评】此题主要考查了仰角的定义及其解直角三角形的应用,解题时首先正确理解仰角的定义,然后利用三角函数和已知条件构造方程解决问题.

练习册系列答案
相关题目
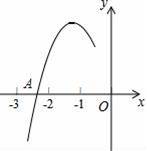


 .在直线l上取点A1,过点A1作x轴的垂线交双曲线于点B1,过点B1作y轴的垂线交直线l于点A2,继续操作:过点A2作x轴的垂线交双曲线于点B2,过点B2作y轴的垂线交直线l于点A3,…,依次这样得到双曲线上的点B1,B2,B3,B4,…,Bn.记点A1的纵坐标为2,则B2016的坐标为 .
.在直线l上取点A1,过点A1作x轴的垂线交双曲线于点B1,过点B1作y轴的垂线交直线l于点A2,继续操作:过点A2作x轴的垂线交双曲线于点B2,过点B2作y轴的垂线交直线l于点A3,…,依次这样得到双曲线上的点B1,B2,B3,B4,…,Bn.记点A1的纵坐标为2,则B2016的坐标为 .




 B.
B.
 C.
C.
 D.
D.



 是下面哪个方程组的解( )
是下面哪个方程组的解( ) B.
B.
 D.
D.



