题目内容
15.先化简,再求值:(1)3a2b-[2ab2-2(-a2b+4ab2)]-5ab2,其中a=-2,b=$\frac{1}{2}$.
(2)2x2-[3(-$\frac{1}{3}$x2+$\frac{2}{3}$xy)-2y2]-2(x2-xy+2y2),其中|x-$\frac{1}{2}$|与(y+1)2互为相反数.
分析 (1)原式去括号合并得到最简结果,把a与b的值代入计算即可求出值;
(2)原式去括号合并得到最简结果,利用非负数的性质求出x与y的值,代入计算即可求出值.
解答 解:(1)原式=3a2b-2ab2-2a2b+8ab2-5ab2=a2b+ab2,
当a=-2,b=$\frac{1}{2}$时,原式=2-$\frac{1}{2}$=1$\frac{1}{2}$;
(2)原式=2x2+x2-2xy+2y2-2x2+2xy-4y2=x2-2y2,
∵|x-$\frac{1}{2}$|与(y+1)2互为相反数,|x-$\frac{1}{2}$|+(y+1)2=0,
∴x=$\frac{1}{2}$,y=-1,
则原式=$\frac{1}{4}$-2=-$\frac{7}{4}$.
点评 此题考查了整式的加减-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
5.抛物线y=-3(x-2)2+4的开口方向和顶点坐标分别是( )
| A. | 向上,(2,4) | B. | 向上,(-2,4) | C. | 向下,(2,4) | D. | 向下,(-2,4) |
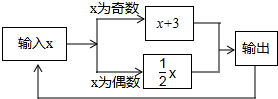 有一数值转换器,原理如图所示,若开始输入x的值是5,可发现第一次输出的结果是8,第二次输出的结果是4,…,请你探索第2015次输出的结果是4.
有一数值转换器,原理如图所示,若开始输入x的值是5,可发现第一次输出的结果是8,第二次输出的结果是4,…,请你探索第2015次输出的结果是4.