题目内容
12．对于二次函数y=（x-1）2+2的图象，下列说法正确的是（ ）| A． | 开口向下 | B． | 对称轴是x=-1 | C． | 与x轴有两个交点 | D． | 顶点坐标是（1，2） |
分析 根据抛物线的性质由a=1得到图象开口向上，根据顶点式得到顶点坐标为（1，2），对称轴为直线x=1，从而可判断抛物线与x轴没有公共点．
解答 解：二次函数y=（x-1）2+2的图象开口向上，顶点坐标为（1，2），对称轴为直线x=1，抛物线与x轴没有公共点．
故选：D．
点评 本题考查了二次函数的性质：二次函数y=ax2+bx+c（a≠0）的顶点式为y=a（x-$\frac{b}{2a}$）2+$\frac{4ac-{b}^{2}}{4a}$，顶点坐标是（-$\frac{b}{2a}$，$\frac{4ac-{b}^{2}}{4a}$），对称轴是直线x=-$\frac{b}{2a}$，当a＞0时，抛物线y=ax2+bx+c（a≠0）的开口向上，当a＜0时，抛物线y=ax2+bx+c（a≠0）的开口向下．
练习册系列答案
相关题目
2．下面画的数轴正确的是（ ）
| A． |  | B． |  | C． |  | D． |  |
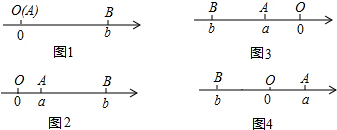
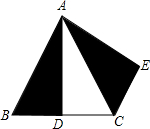如图，△ABC是等边三角形，D是BC的中点，△ABD经过旋转后达到△ACE的位置，请你思考并回答下列问题：