题目内容
7. 如图,在平面直角坐标系中,矩形ABCO的边CO、OA分别在x轴、y轴上,点E在边BC上,将该矩形沿AE折叠,点B恰好落在边OC上的F处.若OA=8,CF=4,则点E的坐标是(-10,3).
如图,在平面直角坐标系中,矩形ABCO的边CO、OA分别在x轴、y轴上,点E在边BC上,将该矩形沿AE折叠,点B恰好落在边OC上的F处.若OA=8,CF=4,则点E的坐标是(-10,3).
分析 根据题意可以得到CE、OF的长度,根据点E在第二象限,从而可以得到点E的坐标.
解答 解:设CE=a,则BE=8-a,
由题意可得,EF=BE=8-a,
∵∠ECF=90°,CF=4,
∴a2+42=(8-a)2,
解得,a=3,
设OF=b,
∵△ECF∽△FOA,
∴$\frac{CE}{OF}=\frac{CF}{OA}$,
即$\frac{3}{b}=\frac{4}{8}$,得b=6,
即CO=CF+OF=10,
∴点E的坐标为(-10,3),
故答案为(-10,3).
点评 本题考查勾股定理的应用,矩形的性质、翻折变化、坐标与图形变化-对称,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.点(5,2)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 将如图所示的“点赞”圈案以点O为中心,顺时针旋转90°后得到的图案是( )
将如图所示的“点赞”圈案以点O为中心,顺时针旋转90°后得到的图案是( )



 如图所示,AD⊥BC,EF⊥BC,∠1=∠2.试探究AB与DG有何位置关系,并说明理由.
如图所示,AD⊥BC,EF⊥BC,∠1=∠2.试探究AB与DG有何位置关系,并说明理由.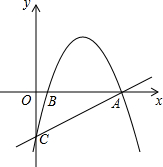 如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点.
如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点.