题目内容
 如图,点O是△ABC内一点,∠A=80°,BO、CO分别是∠ABC和∠ACB的角平分线,则∠BOC等于( )
如图,点O是△ABC内一点,∠A=80°,BO、CO分别是∠ABC和∠ACB的角平分线,则∠BOC等于( )| A、140° | B、120° |
| C、130° | D、无法确定 |
考点:三角形内角和定理
专题:
分析:根据三角形内角和定理求出∠ABC+∠ACB=100°,根据角平分线求出∠OBC=
∠ABC,∠OCB=
∠ACB求出∠OBC+∠OCB=50°,根据三角形的内角和定理求出即可.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵∠A=80°,
∴∠ABC+∠ACB=180°-∠A=100°,
∵BO、CO分别是∠ABC和∠ACB的角平分线,
∴∠OBC=
∠ABC,∠OCB=
∠ACB,
∴∠OBC+∠OCB=50°,
∴∠BOC=180°-(∠OBC+∠OCB)=130°,
故选C.
∴∠ABC+∠ACB=180°-∠A=100°,
∵BO、CO分别是∠ABC和∠ACB的角平分线,
∴∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠OBC+∠OCB=50°,
∴∠BOC=180°-(∠OBC+∠OCB)=130°,
故选C.
点评:本题考查了三角形的内角和定理和角平分线定义的应用,注意:三角形的内角和等于180°.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
若点P关于x轴的对称点的坐标是(2,3),则点P关于原点的对称点的坐标是( )
| A、(-3,-2) |
| B、(2,-3) |
| C、(-2,-3) |
| D、(-2,3) |
下列说法正确的是( )
| A、有理数的绝对值为正数 |
| B、如果两数之和为0,则这两个数的绝对值相等 |
| C、只有正数或负数才有相反数 |
| D、任何数都有倒数 |
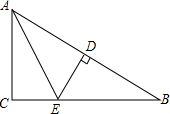 如图所示,在△ABC中,AC⊥BC,AE为∠BAC的平分线,DE⊥AB,AB=7cm,AC=3cm,则BD等于( )
如图所示,在△ABC中,AC⊥BC,AE为∠BAC的平分线,DE⊥AB,AB=7cm,AC=3cm,则BD等于( )| A、1cm | B、2cm |
| C、3cm | D、4cm |