题目内容
已知抛物线y=ax2+bx+c(a>0)的顶点为C点,与x轴交于A(m-2,0)、B(m+2,0)两点,且AC⊥BC.
(1)求a的值;
(2)设抛物线交y轴正半轴于D点,问是否存在实数m,使得△BOD与△ABC相似?若存在,求出m的值;若不存在,说明理由;
(3)当0≤x≤1时,y有最小值为-1,求m的值.
(1)求a的值;
(2)设抛物线交y轴正半轴于D点,问是否存在实数m,使得△BOD与△ABC相似?若存在,求出m的值;若不存在,说明理由;
(3)当0≤x≤1时,y有最小值为-1,求m的值.
考点:二次函数综合题
专题:
分析:(1)先由抛物线y=ax2+bx+c(a>0)与x轴交于A(m-2,0)、B(m+2,0)两点,可设抛物线的解析式为y=a(x-m+2)(x-m-2)=a(x-m)2-4a,再由AC⊥BC,根据抛物线的对称性得出△ABC是等腰直角三角形,由等腰直角三角形的性质得出|-4a|=
AB=2,结合a>0即可求出a=
;
(2)先由抛物线y=
(x-m)2-2交y轴正半轴于D点,得出D(0,
m2-2),OD=
m2-2.再由△ABC是等腰直角三角形,得到当△BOD与△ABC相似时,△BOD也是等腰直角三角形,于是OD=OB.然后分m+2>0;m+2<0;m+2=0三种情况进行讨论;
(3)先由二次函数的性质得出函数y=
(x-m)2-2,当x=m时,y有最小值为-2.根据题目条件0≤x≤1时,y有最小值为-1,可知m<0或m>1.再分m<0;m>1两种情况进行讨论.
| 1 |
| 2 |
| 1 |
| 2 |
(2)先由抛物线y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)先由二次函数的性质得出函数y=
| 1 |
| 2 |
解答:解:(1)∵抛物线y=ax2+bx+c(a>0)与x轴交于A(m-2,0)、B(m+2,0)两点,
∴可设抛物线的解析式为y=a(x-m+2)(x-m-2)=a(x-m)2-4a,
∴顶点C(m,-4a),
∵AC⊥BC,
∴△ABC是等腰直角三角形,
∵AB=4,
∴|-4a|=
AB=2,
∴a=
;
(2)∵抛物线y=
(x-m)2-2交y轴正半轴于D点,
∴D(0,
m2-2),OD=
m2-2.
∵△ABC是等腰直角三角形,
∴当△BOD与△ABC相似时,△BOD也是等腰直角三角形,
∴OD=OB.
①当m+2>0时,
m2-2=m+2,解得m1=4,m2=-2(不合题意舍去);
②当m+2<0时,
m2-2=-(m+2),解得m1=0,m2=-2(均不合题意,都舍去);
③当m+2=0即m=-2时,B、O、D三点重合,(不合题意舍去);
综上所述,存在实数m=4,使得△BOD与△ABC相似;
(3)∵y=
(x-m)2-2,
∴当x=m时,y有最小值为-2.
∵当0≤x≤1时,y有最小值为-1,
∴m<0或m>1.
①当m<0时,顶点(对称轴x=m)在0≤x≤1范围左侧,
此时函数在0≤x≤1范围内y随着x的增大增大,所以当x=0时,y最小,
所以-1=
(0-m)2-2,
解得m=±
,
因m<0,所以m=-
;
②当m>1时,顶点(对称轴x=m)在0≤x≤1范围右侧,
此时函数在0≤x≤1范围内y随着x的增大而减小,
所以当x=1时,y最小,
所以-1=
(1-m)2-2,
解得m=1±
,
因m>1,所以m=1+
;
综上所述,m的值为-
或1+
.
∴可设抛物线的解析式为y=a(x-m+2)(x-m-2)=a(x-m)2-4a,
∴顶点C(m,-4a),
∵AC⊥BC,
∴△ABC是等腰直角三角形,
∵AB=4,
∴|-4a|=
| 1 |
| 2 |
∴a=
| 1 |
| 2 |
(2)∵抛物线y=
| 1 |
| 2 |
∴D(0,
| 1 |
| 2 |
| 1 |
| 2 |
∵△ABC是等腰直角三角形,
∴当△BOD与△ABC相似时,△BOD也是等腰直角三角形,
∴OD=OB.
①当m+2>0时,
| 1 |
| 2 |
②当m+2<0时,
| 1 |
| 2 |
③当m+2=0即m=-2时,B、O、D三点重合,(不合题意舍去);
综上所述,存在实数m=4,使得△BOD与△ABC相似;
(3)∵y=
| 1 |
| 2 |
∴当x=m时,y有最小值为-2.
∵当0≤x≤1时,y有最小值为-1,
∴m<0或m>1.
①当m<0时,顶点(对称轴x=m)在0≤x≤1范围左侧,
此时函数在0≤x≤1范围内y随着x的增大增大,所以当x=0时,y最小,
所以-1=
| 1 |
| 2 |
解得m=±
| 2 |
因m<0,所以m=-
| 2 |
②当m>1时,顶点(对称轴x=m)在0≤x≤1范围右侧,
此时函数在0≤x≤1范围内y随着x的增大而减小,
所以当x=1时,y最小,
所以-1=
| 1 |
| 2 |
解得m=1±
| 2 |
因m>1,所以m=1+
| 2 |
综上所述,m的值为-
| 2 |
| 2 |
点评:本题是二次函数的综合题型,其中涉及到的知识点有运用待定系数法求二次函数的解析式,抛物线的对称性、增减性,最值的求法,等腰直角三角形的判定与性质,相似三角形的性质,综合性较强,难度适中.进行分类讨论是解题的关键.

练习册系列答案
相关题目
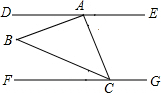 如图,DE∥FG,点A在直线DE上,点C在直线FG上,∠BAC=90°,AB=AC.若∠BCF=20°,则∠EAC的度数为( )
如图,DE∥FG,点A在直线DE上,点C在直线FG上,∠BAC=90°,AB=AC.若∠BCF=20°,则∠EAC的度数为( )| A、25° | B、65° |
| C、70° | D、75° |
某市2013年一季度完成GDP共320亿元,将这一数据用科学记数法表示为( )
| A、3.2×109元 |
| B、3.2×1010元 |
| C、32×109元 |
| D、32×1010元 |
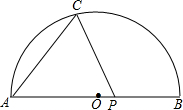 如图,AB为半圆的直径,AB=10,点O到弦AC的距离为4,点P从B出发沿BA方向向点A以每秒1个单位长度的速度运动,连接CP,经过
如图,AB为半圆的直径,AB=10,点O到弦AC的距离为4,点P从B出发沿BA方向向点A以每秒1个单位长度的速度运动,连接CP,经过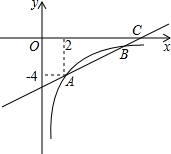 如图,一次函数y=kx+b的图象交反比例函数y=
如图,一次函数y=kx+b的图象交反比例函数y=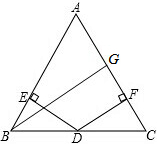 如图,△ABC中,AB=AC,D在BC上(D不在BC中点),DE⊥AB于E,DF⊥AC于F,BG⊥AC于G,求证:DE+DF=BG.
如图,△ABC中,AB=AC,D在BC上(D不在BC中点),DE⊥AB于E,DF⊥AC于F,BG⊥AC于G,求证:DE+DF=BG. 如图,在△ABC中,∠BAC=70°,AB=AC,O为△ABC的外心,△OCP为等边三角形,OP与AC相交于D点,连接OA.
如图,在△ABC中,∠BAC=70°,AB=AC,O为△ABC的外心,△OCP为等边三角形,OP与AC相交于D点,连接OA.