题目内容
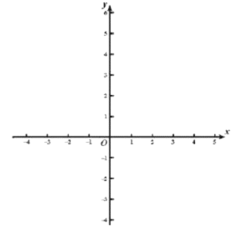
【题目】如图①,在![]() 中,
中,![]() ,
,![]() .点
.点![]() 分别是边
分别是边![]() 上的动点,连接
上的动点,连接![]() .设
.设![]() (
(![]() ),
),![]() ,
,![]() 与
与![]() 之间的函数关系如图②所示.
之间的函数关系如图②所示.
(1)求出图②中线段![]() 所在直线的函数表达式;
所在直线的函数表达式;
(2)将![]() 沿
沿![]() 翻折,得
翻折,得![]() .
.
①点![]() 是否可以落在
是否可以落在![]() 的某条角平分线上?如果可以,求出相应
的某条角平分线上?如果可以,求出相应![]() 的值;如果不可以,说明理由;
的值;如果不可以,说明理由;
②直接写出![]() 与
与![]() 重叠部分面积的最大值及相应
重叠部分面积的最大值及相应![]() 的值.
的值.
【答案】(1)![]() ;(2)①
;(2)①![]() 或
或![]() ;②
;②![]() 与
与![]() 重叠部分面积的最大值为8,此时x=4.
重叠部分面积的最大值为8,此时x=4.
【解析】
(1)利用待定系数法将(3,4)和(6,0)代入y=kx+b即可求得直线函数关系式;
(2)①根据题意可证△DCE∽△ACB,进而可得点M在CT上,且点M不在∠ACB的平分线上,接下来分类讨论,当点M在∠CAB的平分线上或在∠CBA的平分线上时,画出相应的示意图,利用角平分线定理计算即可;
②首先考虑当点M与点T重合时的x的值,进而对x分类讨论,画出相应的示意图,利用相似三角形的性质把重叠部分的面积表示出来,再利用二次函数的顶点式即可求得最大值.
解:(1)设直线PQ为y=kx+b,
将(3,4)和(6,0)代入,得
![]()
解得: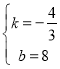
∴直线PQ为![]() ;
;
(2)①过点C作CT⊥AB,垂足为点T,
∵![]() ,
,![]()
∴在Rt△ABC中,![]() ,
,
∵![]()
∴![]()
∴![]() ,
,
∴在Rt△ACT中,![]() ,
,
∴![]() ,
,
由(1)可知![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴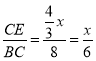 ,
,
∵![]() ,
,
∴![]() ,
,
又∵∠DCE=∠ACB,
∴△DCE∽△ACB,
∴∠DEC=∠ABC,
∴DE∥AB,
∵折叠,
∴点M在CT上,且点M不在∠ACB的平分线上,
∵![]() ,
,
∴在Rt△CDE中,![]() ,
,
∵![]()
∴![]()
∴![]()
∴![]() ,
,![]() ,
,
如图,当点M在∠CAB的平分线上时,即AM平分∠CAT,
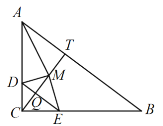
∴![]()
∴![]() ,
,
∴![]() ,
,
∴![]()
∴![]()
解得![]() ,
,
如图,当点M在∠CBA的平分线上时,即BM平分∠CBT,
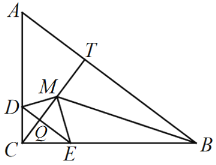
∴![]()
∴![]() ,
,
∴![]() ,
,
∴![]()
∴![]()
解得![]() ,
,
综上所述,x的值为![]() 或
或![]() ;
;
②设![]() 与
与![]() 重叠部分面积为S,
重叠部分面积为S,
如图,当点M与点T重合时,
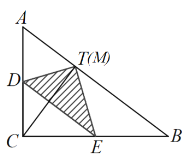
∵折叠,
∴CD=DT,
∴∠DCT=∠DTC,
∵∠ATC=90°,
∴∠DCT=∠A90°,∠DTC=∠DTA=90°,
∴∠A=∠DTA,
∴DA=DT,
∴DA=DC=![]() AC=3,
AC=3,
∴当0<x≤3时,如图,
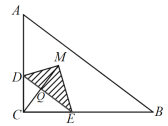
则![]()
![]()
![]()
∵0<x≤3,
∴当x=3时,S取得最大值,最大值为6,
当3<x≤6时,如图,
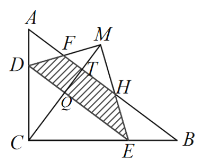
∵![]() ,
,![]()
∴![]() ,
,
∵DE∥AB,
∴![]() ,
,
∴![]() ,
,
∴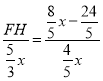 ,
,
∴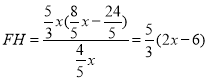 ,
,
∵![]() ,
,![]()
∴![]()
∴![]()
![]()
![]()
![]()
![]() ,
,
∴当x=4时,S取得最大值,最大值为8,
综上所述,![]() 与
与![]() 重叠部分面积的最大值为8,此时x=4.
重叠部分面积的最大值为8,此时x=4.

【题目】多肉植物由于体积小、外形萌,近年来受到广大养花爱好者的青睐.创业青年小宇利用这个商机,去花卉市场选购各种多肉,了解到甲、乙、丙三种多肉的部分价格如下表.
多肉种类 价格 | 甲 | 乙 | 丙 |
批发价(元/株) |
| ||
零售价(元/株) |
|
|
|
(1)已知小宇第一次批发购进甲多肉![]() 株,乙多肉
株,乙多肉![]() 株,共花费
株,共花费![]() 元,且甲多肉每株的批发价比乙多肉低
元,且甲多肉每株的批发价比乙多肉低![]() 元,求甲多肉、乙多肉每株的批发价.
元,求甲多肉、乙多肉每株的批发价.
(2)由于销量好,第一次多肉全部售完,小宇用第一次的销售收入再批发甲、乙、丙三种多肉,且购进甲、乙多肉的株数相等,但乙多肉的批发价每株比原来降低![]() ,甲多肉的批发价,每株比原来提高
,甲多肉的批发价,每株比原来提高![]() .
.
①若他第二次批发购进甲、乙两种多肉分别花费![]() 元、
元、![]() 元,求
元,求![]() 的值.
的值.
②在![]() 的值不变的前提下,小宇把第一次的销售收入全用于第二次多肉批发,若第二次销售完这三种多肉所得利润为
的值不变的前提下,小宇把第一次的销售收入全用于第二次多肉批发,若第二次销售完这三种多肉所得利润为![]() 元,当丙多肉的株数不少于
元,当丙多肉的株数不少于![]() 时,求
时,求![]() 的最大值.
的最大值.