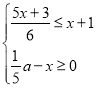��Ŀ����
����Ŀ����һ��ƻ�����A��B������Ṳ42����Ϊ��ҵ��Ʒ�����������ĵ��۷ֱ���50Ԫ��40Ԫ������ѧ�����������ϲ�ò�ͬ���������֪�������A����������Ҫ����B�����������![]() �����ֲ�����B�����������
�����ֲ�����B�����������![]() ���������A�����x�ᣬ����������Ṳ����yԪ��
���������A�����x�ᣬ����������Ṳ����yԪ��
��1����ƻ������������������ķ���y��Ԫ������x���ᣩ�ĺ�����ϵʽ��
��2����ί������ֲ�ͬ�Ĺ�����
��3���̵�Ϊ�˴�����������A�����ÿ������aԪ���ۣ�12��a��18����B�����ÿ������bԪ���ۣ�����ί��ͬѧ�ڸ���ʱ���֣�����������ܷ����빺��ķ����أ����ܷ�������ʱ�����ʱa��ֵ��
���𰸡���1��y��10x+1680����2����6�ֲ�ͬ�Ĺ�������3��a��18��
��������
��1����������õ�y��Ԫ������x���ᣩ�ĺ�����ϵʽ��
��2����������ɵõ�һ������x�IJ���ʽ�飬�����x��ȡֵ��Χ���ٽ�ϻ��ѵĺ���ʽ�������x�ľ�����ֵ��
��3�����ݹ���������ܷ����빺��ķ����ؿɵú�����ϵʽ��x��ϵ��Ϊ0�����ɵõ�a��b�Ĺ�ϵ���ٸ��ݺ�����С����ȷ��a��ȡֵ��Χ�����ɵõ����ۣ�
�⣺��1��������ã�y��50x+40��42��x����
��y��10x+1680��
��2���������
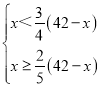 ��
��
���12��x��18��
��x��ȡ12��13��14��15��16��17��
�ʰ�ί����6�ֲ�ͬ�Ĺ�����
��3�����ܷ���Ϊw����������ã�
w��(50��a)x+(40��b) (42��x)��
w��(50��a)x+42(40��b)��(40��b)x��
w��(10��a+b��x+42(40��b)��
�߹���������ܷ����빺��ķ����أ���w��ֵ��x�أ�
��10��a+b��0��
��b��a��10��
��w��42[40��(a��10)]����42a+2100��
�ߩ�42��0����w��a�������С��
�֡�12��a��18��
��a��18ʱ��w��С��1354��Ԫ��
����a��18��

 ��ְٷְټ���ϵ�д�
��ְٷְټ���ϵ�д� �����ƻ���ĩ��̶�100��ϵ�д�
�����ƻ���ĩ��̶�100��ϵ�д� �ܿ���ȫ��100��ϵ�д�
�ܿ���ȫ��100��ϵ�д�