题目内容
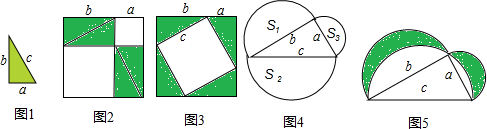
 请你观察图形,依据图形面积之间的关系,不需要连其他的线,便可得到一个你非常熟悉的公式,这个公式是
请你观察图形,依据图形面积之间的关系,不需要连其他的线,便可得到一个你非常熟悉的公式,这个公式是
- A.(a+b)(a-b)=a2-b2
- B.(a+b)2=a2+2ab+b2
- C.(a-b)2=a2-2ab+b2
- D.(a+b)2=a2+ab+b2
B
分析:此题观察一个正方形被分为四部分,把这四部分的面积相加就是边长为a+b的正方形的面积,从而得到一个公式.
解答:由图知,大正方形的边长为a+b,
∴大正方形的面积为,(a+b)2,
根据图知,大正方形分为:一个边长为a的小正方形,一个边长为b的小正方形,
两个长为b,宽为a的长方形,
∵大正方形的面积等于这四部分面积的和,
∴(a+b)2=a2+2ab+b2,
故选B.
点评:此题比较新颖,用面积分割法来证明完全平方式,主要考查完全平方式的展开式.
分析:此题观察一个正方形被分为四部分,把这四部分的面积相加就是边长为a+b的正方形的面积,从而得到一个公式.
解答:由图知,大正方形的边长为a+b,
∴大正方形的面积为,(a+b)2,
根据图知,大正方形分为:一个边长为a的小正方形,一个边长为b的小正方形,
两个长为b,宽为a的长方形,
∵大正方形的面积等于这四部分面积的和,
∴(a+b)2=a2+2ab+b2,
故选B.
点评:此题比较新颖,用面积分割法来证明完全平方式,主要考查完全平方式的展开式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


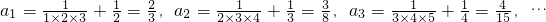 ,依据上述规律,则a99=______;
,依据上述规律,则a99=______;
 ,
, ,
, ,…,根据观察计算:
,…,根据观察计算: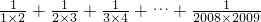 .
.