Question

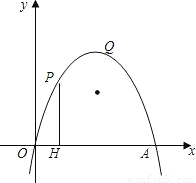
（2009•永嘉县二模）如图，抛物线y=-x²+mx过点A（4，0），O为坐标原点，Q是抛物线的顶点．
（1）求m的值和顶点Q的坐标；
（2）设点P是x轴上方抛物线上的一个动点，过点P作PH⊥x轴，H为垂足，求折线P-H-O长度的最大值．

Answer 1

【答案】分析：（1）因为抛物线y=-x²+mx过点A（4，0），所以把此点代入抛物线的解析式即可求出m的值，从而求出其解析式．根据顶点坐标公式即可求出其顶点坐标；
（2）根据抛物线的解析式，设出P点坐标，即可列出直线l长度的解析式，根据此解析式即可求出l的最大值．
解答：解：（1）把点A（4，0）抛物线y=-x²+mx
得，-16+4m=0，
解得m=4，
故此抛物线的解析式为y=-x²+4x．（3分）
Q点坐标为x=-=-=2，y===4．（6分）

（2）设点P（x，-x²+4x），
则折线P-H-O的长度：l=-x²+5x=-（x-）²+
∴折线P-H-O的长度的最大值为．（12分）
点评：此题考查的是二次函数图象上点的坐标特征，属二次函数部分较为简单题目．