题目内容
5.已知函数y=mx2-2mx-1(m是常数,且≠0),下列结论正确的是( )| A. | 当m=-2时,函数图象与x轴没有交点 | |
| B. | 当m=1时,函数图象过点(-1,1) | |
| C. | 若m<0,则当x≤1时,y随x的增大而增大 | |
| D. | 若m>0,则当x≥1时,y随x的增大而减小 |
分析 根据△=b2-4ac进行判断则可判断A;把m=1,x=-1代入求得函数值,即可判断B,求得对称轴为x=1,根据二次函数的性质即可判断C、D.
解答 解:∵△=b2-4ac=4m2+4m,
当m=-2时,4m2+4m=4×4+4×(-2)=8>0,
∴图象与x轴的交点有2个,故A错误;
∵当m=1时,y=x2-2x-1,
把x=-1代入得y=2,
∴函数图象过点(-1,2),故B错误;
∵y=mx2-2mx-1=m(x-1)2-m-1,
∵抛物线的对称轴为x=1,
∴若m<0,则当x≤1时,y随x的增大而增大,若m>0,则当x≥1时,y随x的增大而增大,
故C正确,D错误;
故选C.
点评 本题考查了二次函数的性质以及根的判别式,解题的关键是根据对称轴公式求得对称轴.

练习册系列答案
相关题目
20.使式子$\frac{\sqrt{2-x}}{x}$有意义的实数x的取值范围是( )
| A. | x≤2 | B. | x<2且x≠0 | C. | x≤2且x≠0 | D. | x<2 |
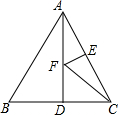 如图,等边△ABC中,AB=4,AD⊥BC于点D,点F在线段AD上运动,点E在AC上,且AE=2,当EF+CF取最小值时,∠ECF=30°.
如图,等边△ABC中,AB=4,AD⊥BC于点D,点F在线段AD上运动,点E在AC上,且AE=2,当EF+CF取最小值时,∠ECF=30°.