题目内容
10.已知m=1+$\sqrt{2}$,n=1-$\sqrt{2}$,则代数式$\sqrt{{m}^{2}+{n}^{2}-mn}$的值$\sqrt{7}$.分析 把所求的式子化成$\sqrt{(m+n)^{2}-3mn}$的形式,然后代入求解即可.
解答 解:原式=$\sqrt{(m+n)^{2}-3mn}$=$\sqrt{{2}^{2}-3(1+\sqrt{2})(1-\sqrt{2})}$=$\sqrt{4+3}$=$\sqrt{7}$.
故答案是:$\sqrt{7}$.
点评 本题考查了二次根式的化简求值,正确理解完全平方公式,对所求的式子进行变形是关键.

练习册系列答案
相关题目
6.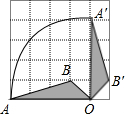 如图,在5×5的正方形网格中,每个小正方形的边长都为1,若将△AOB绕点O顺时针旋转90°得到△A′OB′,则A点运动的路径$\widehat{AA′}$的长为( )
如图,在5×5的正方形网格中,每个小正方形的边长都为1,若将△AOB绕点O顺时针旋转90°得到△A′OB′,则A点运动的路径$\widehat{AA′}$的长为( )
 如图,在5×5的正方形网格中,每个小正方形的边长都为1,若将△AOB绕点O顺时针旋转90°得到△A′OB′,则A点运动的路径$\widehat{AA′}$的长为( )
如图,在5×5的正方形网格中,每个小正方形的边长都为1,若将△AOB绕点O顺时针旋转90°得到△A′OB′,则A点运动的路径$\widehat{AA′}$的长为( )| A. | π | B. | 2π | C. | 4π | D. | 8π |
20.下列计算结果为负数的是( )
| A. | |-3| | B. | (-3)0 | C. | -(+3) | D. | (-3)2 |
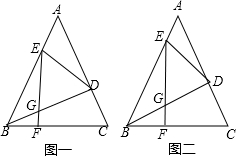
 如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于点E,交BC于点D,连接BE、AD交于点P,求证:
如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于点E,交BC于点D,连接BE、AD交于点P,求证: 如图,在矩形ABCD中,$\frac{AB}{BC}=\frac{3}{5}$,AC为对角线,BM⊥AC于点M,交AD于点N,点O是BC边上一点,$\frac{OC}{BC}=\frac{1}{3}$,连接DO交AC于点P,OF⊥OD交BN于点E,交AB边于点F.
如图,在矩形ABCD中,$\frac{AB}{BC}=\frac{3}{5}$,AC为对角线,BM⊥AC于点M,交AD于点N,点O是BC边上一点,$\frac{OC}{BC}=\frac{1}{3}$,连接DO交AC于点P,OF⊥OD交BN于点E,交AB边于点F.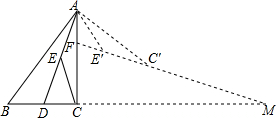 在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AD平分∠CAB交BC于点D,E为AD的中点,连接CE,将△ACE绕点A逆时针旋转至△AE′C′,直线E′C′交AC于点F,交BC的延长线于点M,若AF=E′F,则CM=$\frac{96-10\sqrt{10}}{7}$.
在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AD平分∠CAB交BC于点D,E为AD的中点,连接CE,将△ACE绕点A逆时针旋转至△AE′C′,直线E′C′交AC于点F,交BC的延长线于点M,若AF=E′F,则CM=$\frac{96-10\sqrt{10}}{7}$.