Question

【题目】阅读下列材料，并完成相应任务．

古希腊数学家，天文学家欧多克索斯（Eudoxus，约前400—前347）曾提出：能否将一

条线段分成不相等的两部分．使较短线段与较长线段的比等于较长线段与原线段的比，这个相等的比就是，黄金分割在我们生活中有广泛运用．黄金分割点也可以用折纸的方式得到．

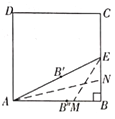
第一步：裁一张正方形的纸片，先折出的中点，然后展平，再折出线段，再展平；

第二步：将纸片沿折叠，使落到线段上，的对应点为，展平；

第三步：沿折叠，使落在上，的对应点为，展平，这时就是的黄金分割点．

古希腊数学家，天文学家欧多克索斯（Eudoxus，约前400—前347）曾提出：能否将一

条线段分成不相等的两部分．使较短线段与较长线段的比等于较长线段与原线段的比，这个相等的比就是，黄金分割在我们生活中有广泛运用．黄金分割点也可以用折纸的方式得到．

第一步：裁一张正方形的纸片，先折出的中点，然后展平，再折出线段，再展平；

第二步：将纸片沿折叠，使落到线段上，的对应点为，展平；

第三步：沿折叠，使落在上，的对应点为，展平，这时就是的黄金分割点．

任务：（1）试根据以上操作步骤证明就是的黄金分割点；

（2）请写出一个生活中应用黄金分割的实际例子．

Answer 1

【答案】（1）证明见解析；（2）答案不唯一．如：节目主持人报幕，总是站在舞台上侧近于0.618的位置才是最佳的位置；时装模特、舞蹈演员腿长和身高的比例也近似于0.618比值．

【解析】

（1）根据操作步骤先设正方形的边长为，然后利用勾股定理结合折叠的特点求解（2）生活中的例子很多，选择其中一个例子即可.

解：（1）证明：设正方形的边长为，

∵为的中点，

∴，

∴．

又∵由折叠可得，

∴，

又∵，

∴，

∴点是线段的黄金分割点．

（2）答案不唯一．如：节目主持人报幕，总是站在舞台上侧近于0.618的位置才是最佳的位置；时装模特、舞蹈演员腿长和身高的比例也近似于0.618比值．