题目内容
14.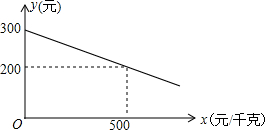 某企业生产一种环保产品,需要添加一种稀少材料的新型原料,若每件产品的利润与新型原料价格成一次函数关系,且每件产品的利润y(元)与新型原料的价格x(元/千克)的函数图象如图:
某企业生产一种环保产品,需要添加一种稀少材料的新型原料,若每件产品的利润与新型原料价格成一次函数关系,且每件产品的利润y(元)与新型原料的价格x(元/千克)的函数图象如图:(1)当新型原料的价格为400元/千克时,每件产品的利润是多少?
(2)为了珍惜资源,政府部门规定:每天使用量m(千克)与价格x(元/千克)的函数关系为m=$\frac{1}{10}$x-50,且1千克新型原料可生产10件产品.那么生产200件这种产品,一共可得利润是多少?
分析 (1)把(0,300),(500,200)代入直线解析式可得一次函数解析式,把x=400代入函数解析式可得利润的值;
(2)利润=用新型原料量×每千克新型原料产生利润,YC JK QJ.
解答 解:(1)工厂每千克新型原料产生利润y(元/千克)与电价x(元/千克)的函数解析式为:
y=kx+b(k、b是常数,且k≠0).
该函数图象过点(0,300),(500,200),
∴$\left\{\begin{array}{l}{500k+b=200}\\{b=300}\end{array}\right.$
解得$\left\{\begin{array}{l}{k=-\frac{1}{5}}\\{b=300}\end{array}\right.$.
则y=-$\frac{1}{5}$x+300(x≥0).
当新型原料价x=400元/千克时,该工厂消耗每千克新型原料产生利润y=-$\frac{1}{5}$×400+300=220(元/千克).
答:工厂消耗每千克新型原料产生利润是220元.
(2)由m=$\frac{1}{10}$x-50,得x=10m+500,
设工厂每天消耗新型原料产生利润为w元,由题意得:
W=my=m(-$\frac{1}{5}$x+300)=m[-$\frac{1}{5}$(10m+500)+300].
化简配方,得:w=-2(m-50)2+5000.
∵1千克新型原料可生产10件产品,
∴那么生产200件这种产品需要新型原料20千克,
∴当m=20时,w=-2(m-50)2+5000=-2×900+5000=3200(元).
点评 本题考查二次函数及一次函数的应用;得到总利润的等量关系是解决本题的关键;注意利用配方法解决二次函数的最值问题.

练习册系列答案
相关题目
5.2015年8月初,某学生用品专卖店以每个50元的价格购进800个芭蕾牌书包,第一周以单价80元销售,售出了200个;第二周如果单价不变,预计仍可售出200个,该专卖店为了增加销售量.决定从第二周开始降价销售,据市场调查,若单价每降低1元,就可多售出10个,但最低单价应高于购进价.待第二周结束后,专卖店再对剩余书包进行一次性清仓销售,清仓时按进价八折销售,设第二周的单价降低x元.
(1)填写下表(不需要化简)
(2)如果专卖店希望通过销售这批书包获利9000元,那么第二周的单价应是多少?
(1)填写下表(不需要化简)
| 时间 | 第一周 | 第二周 | 清仓 |
| 单价(元) | 80 | 80-x | 40 |
| 销售量(个) | 200 | 200+10x | 400-10x |
2.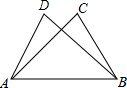 如图,△ABC≌△BAD,点A和点B,点C和点D是对应点,如果AB=6cm,BD=5cm,AD=4cm,那么BC的长是( )
如图,△ABC≌△BAD,点A和点B,点C和点D是对应点,如果AB=6cm,BD=5cm,AD=4cm,那么BC的长是( )
 如图,△ABC≌△BAD,点A和点B,点C和点D是对应点,如果AB=6cm,BD=5cm,AD=4cm,那么BC的长是( )
如图,△ABC≌△BAD,点A和点B,点C和点D是对应点,如果AB=6cm,BD=5cm,AD=4cm,那么BC的长是( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
 如图,中国象棋中的”马“,在图中的坐标为(-1,-1),若”马“再走一步,试写出下一步它可能走到的位置的坐标(0,-3).
如图,中国象棋中的”马“,在图中的坐标为(-1,-1),若”马“再走一步,试写出下一步它可能走到的位置的坐标(0,-3). 如图,一个加油站恰好位于两条公路m,n所夹角的平分线上,若加油站到公路m的距离是80m,则它到公路n的距离是80m.
如图,一个加油站恰好位于两条公路m,n所夹角的平分线上,若加油站到公路m的距离是80m,则它到公路n的距离是80m.