题目内容
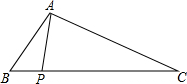 如图,在△ABC中,AB=4,∠ABC=60°,AC=2
如图,在△ABC中,AB=4,∠ABC=60°,AC=2| 19 |
考点:勾股定理
专题:分类讨论
分析:分两种情况进行讨论,①∠APB为钝角,②∠BAP为钝角,分别确定x的范围即可.
解答:解:作AH⊥BC于H,
∵AB=4,∠B=60°,
∴BH=2,AH=2
,
∵AC=3
,
∴HC=8,
即BC=2+8=10,
∵∠B=60°<90°,
∴△ABP为钝角三角形只要分两种情况讨论,
①当∠APB为钝角时,此时可得0<x<2;
②当∠BAP为钝角时,过点A作AP⊥AB,
∵∠B=60°,
即当4<x≤6时,∠BAP为钝角.此时BP=8,
即当8<x≤10时,∠BAP为钝角
综上可得0<x<2或8<x≤10时△ABP为钝角三角形.
∵AB=4,∠B=60°,
∴BH=2,AH=2
| 3 |
∵AC=3
| 19 |

∴HC=8,
即BC=2+8=10,
∵∠B=60°<90°,
∴△ABP为钝角三角形只要分两种情况讨论,
①当∠APB为钝角时,此时可得0<x<2;
②当∠BAP为钝角时,过点A作AP⊥AB,
∵∠B=60°,
即当4<x≤6时,∠BAP为钝角.此时BP=8,
即当8<x≤10时,∠BAP为钝角
综上可得0<x<2或8<x≤10时△ABP为钝角三角形.
点评:此题考查了动点问题的函数图象,有一定难度,解答本题的关键是结合图象及函数图象得出AB、AH的长度,问需要分类讨论,注意不要漏解.

练习册系列答案
 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
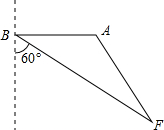 由于过度采伐森林和破坏植被,我国许多地区频频遭受沙尘暴的侵袭,今日A市测得沙尘暴中心在A市的正西方向300km的B处,以10
由于过度采伐森林和破坏植被,我国许多地区频频遭受沙尘暴的侵袭,今日A市测得沙尘暴中心在A市的正西方向300km的B处,以10 如图,为了做好2013年沈阳全运会起降的交通安全工作,某交警执勤小队从A处出发,先到公路l1上设卡检查,再到公路l2上设卡检查,最后再到B地执行任务,他们应如何走才能使总路程最短?
如图,为了做好2013年沈阳全运会起降的交通安全工作,某交警执勤小队从A处出发,先到公路l1上设卡检查,再到公路l2上设卡检查,最后再到B地执行任务,他们应如何走才能使总路程最短?