Question

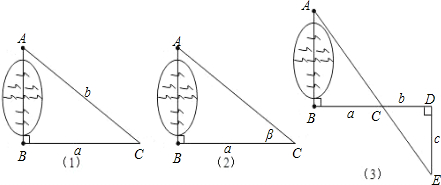
细心观察图形，认真分析各式，然后回答问题：
1+（

1

）²=2S₁=

1

2

1+（

2

）²=3S₂=

2

2

1+（

3

）²=4S₃=

3

2

…
（1）请用含有n（n是正整数）的等式表示上述变化规律______；
（2）推算出OA₁₀的长______；
（3）S₁²+S₂²+S₃²+…+S₁₀²的值等于______．

Answer 1

（1）1+（

1

）²=2，S₁=

1

2

；1+（

2

）²=3，S₂=

2

2

；1+（

3

）²=4，S₃=

3

2

…S_n=

n

2

，
（2）OA₂=

OA12+A1A22

=

2

，OA₃=

3

，…OA₁₀=

10

；
（3）S12=

1

4

，S22=

2

4

，S32=

3

4

，…Sn2=

n

4

，
S₁²+S₂²+S₃²+…+S_n²=

1

4

+

2

4

+…+

n

4

=

n(n+1)

8

，
当n=10时，S₁²+S₂²+S₃²+…+S₁₀²=

55

4

．
故答案为：S_n=

n

2

；

10

；

55

4

．