题目内容
两同心圆的半径分别是10和6,大圆的弦AB长16.AB与小圆的位置关系是________.
相切
分析:过O作OC⊥AB于C,连接OB,根据垂径定理求出BC,根据勾股定理求出OC,和小圆的半径半径即可.
解答:
过O作OC⊥AB于C,连接OB,
∵OC⊥AB,OC过圆心O,
∴AC=BC= AB=8,
AB=8,
在Rt△BOC中,由勾股定理得:OC= =
=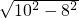 =6,
=6,
即O到AB的距离等于小圆的半径,
∴AB与小圆的位置关系是相切,
故答案为:相切.
点评:本题考查了垂径定理,勾股定理,直线与圆的位置关系的应用,注意:当圆心到直线的距离等于圆的半径时,直线与圆相切.
分析:过O作OC⊥AB于C,连接OB,根据垂径定理求出BC,根据勾股定理求出OC,和小圆的半径半径即可.
解答:

过O作OC⊥AB于C,连接OB,
∵OC⊥AB,OC过圆心O,
∴AC=BC=
 AB=8,
AB=8,在Rt△BOC中,由勾股定理得:OC=
 =
=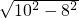 =6,
=6,即O到AB的距离等于小圆的半径,
∴AB与小圆的位置关系是相切,
故答案为:相切.
点评:本题考查了垂径定理,勾股定理,直线与圆的位置关系的应用,注意:当圆心到直线的距离等于圆的半径时,直线与圆相切.

练习册系列答案
相关题目
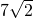 的弦所在直线与小圆的位置关系是________.
的弦所在直线与小圆的位置关系是________. 的弦所在直线与小圆的位置关系是 .
的弦所在直线与小圆的位置关系是 .