题目内容
定义:如果一元二次方程ax2+bx+c=0(a≠0)满足a+b+c=0,那么我们称这个方程为“和谐”方程;如果一元二次方程ax2+bx+c=0(a≠0)满足a﹣b+c=0那么我们称这个方程为“美好”方程,如果一个一元二次方程既是“和谐”方程又是“美好”方程,则下列结论正确的是( )
A. 方有两个相等的实数根 B. 方程有一根等于0
C. 方程两根之和等于0 D. 方程两根之积等于0
C 【解析】试题分析:根据已知得出方程ax2+bx+c=0(a≠0)有两个根x=1和x=﹣1,再判断即可. 【解析】 ∵把x=1代入方程ax2+bx+c=0得出:a+b+c=0, 把x=﹣1代入方程ax2+bx+c=0得出a﹣b+c=0, ∴方程ax2+bx+c=0(a≠0)有两个根x=1和x=﹣1, ∴1+(﹣1)=0, 即只有选项C正确;选项A、B、D都错...
练习册系列答案
相关题目


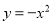 向上平移2个单位,那么所得抛物线与x轴的两个交点之间的距离是____________.
向上平移2个单位,那么所得抛物线与x轴的两个交点之间的距离是____________.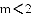
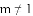
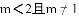
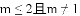
 B.
B.  C.
C.  D.
D. 