题目内容
7.$\sqrt{x-1}+{|{y+3}|^2}=0$,则(-xy)2的值为( )| A. | -6 | B. | 9 | C. | 6 | D. | -9 |
分析 直接利用偶次方的性质以及绝对值的性质化简进而求出答案.
解答 解:∵$\sqrt{x-1}$+|y+3|2=0,
∴x=1,y=-3,
∴(-xy)2=[-1×(-3)]2=9.
故选:B.
点评 此题主要考查了偶次方的性质以及绝对值的性质,正确得出x,y的值是解题关键.

练习册系列答案
相关题目
18. 反比例函数y=$\frac{k}{x}$的图象如图所示,则k的值可能是( )
反比例函数y=$\frac{k}{x}$的图象如图所示,则k的值可能是( )
 反比例函数y=$\frac{k}{x}$的图象如图所示,则k的值可能是( )
反比例函数y=$\frac{k}{x}$的图象如图所示,则k的值可能是( )| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | -1 |
12.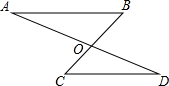 如图,已知AB∥CD,AD与BC相交于点O,∠B=40°,∠D=34°,则∠AOC=( )
如图,已知AB∥CD,AD与BC相交于点O,∠B=40°,∠D=34°,则∠AOC=( )
 如图,已知AB∥CD,AD与BC相交于点O,∠B=40°,∠D=34°,则∠AOC=( )
如图,已知AB∥CD,AD与BC相交于点O,∠B=40°,∠D=34°,则∠AOC=( )| A. | 40° | B. | 34° | C. | 74° | D. | 90° |
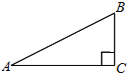 如图,在Rt△ABC中,∠ABC=90°,BC=1,AC=$\sqrt{5}$.
如图,在Rt△ABC中,∠ABC=90°,BC=1,AC=$\sqrt{5}$.
 如图,已知点D、E是△ABC的边BC上两点,且BD=CE,∠1=∠2.试证:△ABC是等腰三角形.
如图,已知点D、E是△ABC的边BC上两点,且BD=CE,∠1=∠2.试证:△ABC是等腰三角形.