题目内容
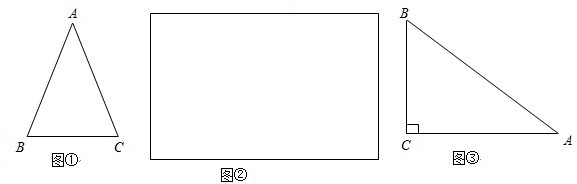
定义：在等腰三角形中，底边与腰的比叫做顶角的正对，记作：sad．例如：在图①的等腰△ABC中，AB=AC，顶角A的正对记作sadA，这时sadA=
=
．根据上述角的正对定义，解下列问题：
（1）sad60°=
（2）求sad90°的值（请先在图②的方框内，画出符合题意的图形，再根据图形求解）．
（3）如图③，已知sinA=
，其中∠A为锐角，试求sadA的值．
| 底边 |
| 腰 |
| BC |
| AB |
（1）sad60°=
1
1
．（2）求sad90°的值（请先在图②的方框内，画出符合题意的图形，再根据图形求解）．
（3）如图③，已知sinA=
| 3 |
| 5 |
分析：（1）根据有一个角为60°的等腰三角形为等边三角形得到底与腰相等，即可求出sad60°的值；
（2）如图②所示，设AB=AC=x，利用勾股定理表示出BC，求出底边与腰之和即为sad90°的值；
（3）如图所示，过C作CE垂直于AB，截取AF=AC，连接CF，在Rt△ABC中，根据sinA的值，设出BC与AB，表示出AC，再由面积法表示出CE，由AF-AE表示出EF，利用勾股定理表示出CF，由CF与AC的比值即为sadA的值．
（2）如图②所示，设AB=AC=x，利用勾股定理表示出BC，求出底边与腰之和即为sad90°的值；
（3）如图所示，过C作CE垂直于AB，截取AF=AC，连接CF，在Rt△ABC中，根据sinA的值，设出BC与AB，表示出AC，再由面积法表示出CE，由AF-AE表示出EF，利用勾股定理表示出CF，由CF与AC的比值即为sadA的值．
解答：
解：（1）sad 60°=1；
（2）画图：画△ABC，使得∠A=90°，且AB=AC，
sad 90°=
，
理由：在△ABC，∠A=90°，AB=AC，
（设：AB=AC=x），
∴BC=
=
x，
∴sad 90°=
=
=
=
；
（3）过点C作CE⊥AB于点E，在AB上截取AF=AC，连接CF，如图所示，
∵sinA=
，
∴设BC=3k，AB=5k，则AC=4K，
∴AF=AC=4k，
∵S△ABC=
AC•BC=
AB•CE，
∴AC•BC=AB•CE，即3k•4k=5k•CE，
∴CE=2.4K，
在Rt△ACE中，AE=
=3.2k，
∴EF=AF-AE=4k-3.2k=0.8k，
在Rt△CEF中，CF=
=
k，
在等腰三角形ACF中，sadA=
=
=
．
解：（1）sad 60°=1；（2）画图：画△ABC，使得∠A=90°，且AB=AC，
sad 90°=
| 2 |
理由：在△ABC，∠A=90°，AB=AC，
（设：AB=AC=x），
∴BC=
| AB2+AC2 |
| 2 |
∴sad 90°=
| 底边 |
| 腰 |
| BC |
| AB |
| ||
| x |
| 2 |
（3）过点C作CE⊥AB于点E，在AB上截取AF=AC，连接CF，如图所示，
∵sinA=
| 3 |
| 5 |
∴设BC=3k，AB=5k，则AC=4K，
∴AF=AC=4k，
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴AC•BC=AB•CE，即3k•4k=5k•CE，
∴CE=2.4K，
在Rt△ACE中，AE=
| AC2-CE2 |
∴EF=AF-AE=4k-3.2k=0.8k，
在Rt△CEF中，CF=
| EC2+FE2 |
4
| ||
| 5 |
在等腰三角形ACF中，sadA=
| CF |
| AC |
| ||||
| 4k |
| ||
| 5 |
点评：此题属于解直角三角形题型，涉及的知识有：勾股定理，锐角三角函数定义，弄清题中的新定义是解本题的关键．
练习册系列答案
阶梯计算系列答案
相关题目
互唯一确定的．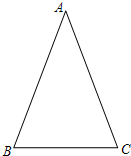
学习过三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化．
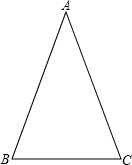
学习过三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化．类似的，也可以在等腰三角形中建立边角之间的联系，我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）．如图，在△ABC中，AB=AC，顶角A的正对记作sadA，这时sad A=
（2014•宝山区一模）通过锐角三角比的学习，我们已经知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长比与角的大小之间可以相互转化．类似的我们可以在等腰三角形中建立边角之间的联系．我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）．如图在△ABC中，AB=AC，