题目内容
如图，梯形ABCD的对角线交于O，过O作两底的平行线分别交两腰于M，N．若AB=4，CD=1，则MN的长为
- A.1.2
- B.1.4
- C.1.6
- D.1.8
C
分析：根据题意，可先判断出图中所有的相似三角形，再根据对应边的比相等，利用等比性质即可求得MN的值．
解答：∵MN∥CD
∴△AOM∽△ACD，△BON∽△BCD，△COD∽△AOB
∴
，
，
∴
∴
∴MN=1.6．
故选C．
点评：此题综合运用了相似三角形的对应边的比相等以及等比性质．
分析：根据题意，可先判断出图中所有的相似三角形，再根据对应边的比相等，利用等比性质即可求得MN的值．
解答：∵MN∥CD
∴△AOM∽△ACD，△BON∽△BCD，△COD∽△AOB
∴
，，∴
∴
∴MN=1.6．
故选C．
点评：此题综合运用了相似三角形的对应边的比相等以及等比性质．
练习册系列答案
相关题目
如图，梯形ABCD的对角线交于点O，有以下四个结论：①△AOB∽△COD，②△AOD∽△ACB，③S△DOC：S△AOD=DC：AB，④S△AOD=S△BOC，其中始终正确的有（ ）个．
| A、1 | B、2 | C、3 | D、4 |
14、如图，梯形ABCD的两条对角线交于点E，图中面积相等的三角形共有
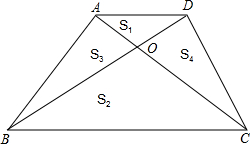如图，梯形ABCD的对角线AC、BD相交于点O，△ADO的面积记作S1，△BCO的面积记作S2，△ABO的面积记作S3，△CDO的面积记作S4，则下列关系正确是（ ）| A、S1=S2 | B、S1×S2=S3×S4 | C、S1+S2=S4+S3 | D、S2=2S3 |
16、如图，梯形ABCD的对角线交于点O，有以下三个结论：
如图，梯形ABCD的面积为34cm2，AE=BF，CE与DF相交于O，△OCD的面积为11cm2，则阴影部分的面积为