题目内容
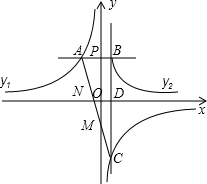 (2013•宜兴市一模)如图,已知反比例函数y1=
(2013•宜兴市一模)如图,已知反比例函数y1=| k1 |
| x |
| k2 |
| x |
| (k1+k2)2 |
| 2k2 |
| (k1+k2)2 |
| 2k2 |
分析:设点B的坐标为(m,
),则可得点A的坐标为(
,
),点C的坐标为(m,
),求出直线AC的解析式,可得出OM的长度,易得△MON∽△CBA,利用面积比等于相似比平方可求出△OMN的面积.
| k2 |
| m |
| mk1 |
| k2 |
| k2 |
| m |
| k1 |
| m |
解答:解:设点B的坐标为(m,
),则可得点A的坐标为(
,
),点C的坐标为(m,
),
设直线AC的解析式为y=ax+b,将A、C的坐标代入可得:
,
解得:
,
故直线AC的解析式为y=-
x+
,
则可得OM=-
,
由B、C的坐标可得BC=
-
=
,由A、B坐标可得AB=m-
=
,
从而可得S△CBA=
AB×BC=
×
×
=
,
∵△△MON∽△CBA,
∴
=(
)2,即
=(
)2,
解得:S△MON=
.
故答案为:
.
| k2 |
| m |
| mk1 |
| k2 |
| k2 |
| m |
| k1 |
| m |
设直线AC的解析式为y=ax+b,将A、C的坐标代入可得:
|
解得:
|
故直线AC的解析式为y=-
| k2 |
| m2 |
| k1+k2 |
| m |
则可得OM=-
| k1+k2 |
| m |
由B、C的坐标可得BC=
| k2 |
| m |
| k1 |
| m |
| k2-k1 |
| m |
| mk1 |
| k2 |
| m(k2-k1) |
| k2 |
从而可得S△CBA=
| 1 |
| 2 |
| 1 |
| 2 |
| k2-k1 |
| m |
| m(k2-k1) |
| k2 |
| (k2-k1)2 |
| 2k2 |
∵△△MON∽△CBA,
∴
| S△MON |
| S△CBA |
| OM |
| BC |
| S△MON | ||
|
-
| ||
|
解得:S△MON=
| (k1+k2)2 |
| 2k2 |
故答案为:
| (k1+k2)2 |
| 2k2 |
点评:本题考查了反比例函数及一次函数的综合题,解答本题的关键是设出各点的坐标,利用相似三角形的面积比等于相似比平方得出关系式求解,计算量较大,注意细心运算.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
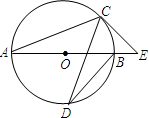 (2013•宜兴市一模)如图,AB是⊙O的直径,C、D是⊙O上的点,∠CDB=20°,过点C作⊙O的切线交AB的延长线于点E,则∠E=
(2013•宜兴市一模)如图,AB是⊙O的直径,C、D是⊙O上的点,∠CDB=20°,过点C作⊙O的切线交AB的延长线于点E,则∠E= (2013•宜兴市一模)如图,在△ABC中,AC=BC>AB,点P为△ABC所在平面内一点,且点P与△ABC的任意两个顶点构成△PAB,△PBC,△PAC均是等腰三角形,则满足上述条件的所有点P的个数为
(2013•宜兴市一模)如图,在△ABC中,AC=BC>AB,点P为△ABC所在平面内一点,且点P与△ABC的任意两个顶点构成△PAB,△PBC,△PAC均是等腰三角形,则满足上述条件的所有点P的个数为 (2013•宜兴市一模)如图,已知△ABC在平面直角坐标系中,其中点A、B、C三点的坐标分别为(1,2
(2013•宜兴市一模)如图,已知△ABC在平面直角坐标系中,其中点A、B、C三点的坐标分别为(1,2