题目内容
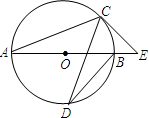（2013•宜兴市一模）如图，AB是⊙O的直径，C、D是⊙O上的点，∠CDB=20°，过点C作⊙O的切线交AB的延长线于点E，则∠E=50°
50°
．分析：首先连接OC，由切线的性质可得OC⊥CE，又由圆周角定理，可求得∠COB的度数，继而可求得答案．
解答：
解：连接OC，
∵CE是⊙O的切线，
∴OC⊥CE，
即∠OCE=90°，
∵∠COB=2∠CDB=40°，
∴∠E=90°-∠COB=50°．
故答案为：50°．
解：连接OC，∵CE是⊙O的切线，
∴OC⊥CE，
即∠OCE=90°，
∵∠COB=2∠CDB=40°，
∴∠E=90°-∠COB=50°．
故答案为：50°．
点评：此题考查了切线的性质与圆周角定理．此题比较简单，注意掌握辅助线的作法，注意数形结合思想的应用．
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
（2013•宜兴市一模）如图，在△ABC中，AC=BC＞AB，点P为△ABC所在平面内一点，且点P与△ABC的任意两个顶点构成△PAB，△PBC，△PAC均是等腰三角形，则满足上述条件的所有点P的个数为
（2013•宜兴市一模）如图，已知△ABC在平面直角坐标系中，其中点A、B、C三点的坐标分别为（1，2