题目内容
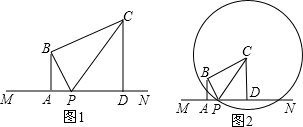
 (2013•宜兴市一模)如图,已知△ABC在平面直角坐标系中,其中点A、B、C三点的坐标分别为(1,2
(2013•宜兴市一模)如图,已知△ABC在平面直角坐标系中,其中点A、B、C三点的坐标分别为(1,2| 3 |
分析:首先根据给出的点的坐标判定三角形ABC是等边三角形,作点B关于AC的对称点E,连接EP、EB、ED、EC,则PB+PD=PE+PD,因此ED的长就是PB+PD的最小值,即当点P运动到ED与AC的交点G时,△PBD的周长最小.
解答: 解:如图,作点B关于AC的对称点E,连接EP、EB、ED、EC,则PB+PD=PE+PD,因此ED的长就是PB+PD的最小值,即当点P运动到ED与AC的交点G时,△PBD的周长最小.
解:如图,作点B关于AC的对称点E,连接EP、EB、ED、EC,则PB+PD=PE+PD,因此ED的长就是PB+PD的最小值,即当点P运动到ED与AC的交点G时,△PBD的周长最小.
∵A、B、C三点的坐标分别为(1,2
),(-1,0),(3,0),点D为BC中点,
∴AB=
=4,BC=4,AC=
=4,
∴△ABC是等边三角形,
从点D作DF⊥BE,垂足为F,因为BC=4,所以BD=2,
BE=2
=4
,
因为∠DBF=30°,所以DF=
BD=1,BF=
,EF=BE-BF=4
-
=3
,DE=
=2
,
所以△PBD的周长的最小值是2+2
,
故选A.
 解:如图,作点B关于AC的对称点E,连接EP、EB、ED、EC,则PB+PD=PE+PD,因此ED的长就是PB+PD的最小值,即当点P运动到ED与AC的交点G时,△PBD的周长最小.
解:如图,作点B关于AC的对称点E,连接EP、EB、ED、EC,则PB+PD=PE+PD,因此ED的长就是PB+PD的最小值,即当点P运动到ED与AC的交点G时,△PBD的周长最小.∵A、B、C三点的坐标分别为(1,2
| 3 |
∴AB=
| 12+4 |
| 12+4 |
∴△ABC是等边三角形,
从点D作DF⊥BE,垂足为F,因为BC=4,所以BD=2,
BE=2
| 42-22 |
| 3 |
因为∠DBF=30°,所以DF=
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
| DF2+EF2 |
| 7 |
所以△PBD的周长的最小值是2+2
| 7 |
故选A.
点评:本题考查了等边三角形的判定和性质以及勾股定理的灵活运用,解本题的关键是作出恰当的图形,并且根据勾股定理求各边长.

练习册系列答案
相关题目
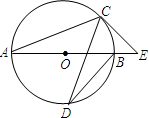 (2013•宜兴市一模)如图,AB是⊙O的直径,C、D是⊙O上的点,∠CDB=20°,过点C作⊙O的切线交AB的延长线于点E,则∠E=
(2013•宜兴市一模)如图,AB是⊙O的直径,C、D是⊙O上的点,∠CDB=20°,过点C作⊙O的切线交AB的延长线于点E,则∠E= (2013•宜兴市一模)如图,在△ABC中,AC=BC>AB,点P为△ABC所在平面内一点,且点P与△ABC的任意两个顶点构成△PAB,△PBC,△PAC均是等腰三角形,则满足上述条件的所有点P的个数为
(2013•宜兴市一模)如图,在△ABC中,AC=BC>AB,点P为△ABC所在平面内一点,且点P与△ABC的任意两个顶点构成△PAB,△PBC,△PAC均是等腰三角形,则满足上述条件的所有点P的个数为