题目内容
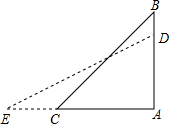 如图,有一直立标杆,它的上部被风从B处吹折,杆顶C着地,离杆脚2m,修好后又被风吹折,因新断处D比前一次低0.5m,故杆顶E着地比前次远1m,求原标杆的高度.
如图,有一直立标杆,它的上部被风从B处吹折,杆顶C着地,离杆脚2m,修好后又被风吹折,因新断处D比前一次低0.5m,故杆顶E着地比前次远1m,求原标杆的高度.考点:勾股定理的应用
专题:
分析:由题中条件,可设原标杆AB的高为x,进而再依据勾股定理建立平衡方程,进而求解即可.
解答:解:依题意得AC=2,AE=3,
设原标杆的高为x,
∵∠A=90°,
∴由题中条件可得AB2+AC2=BC2,即AB2+22=(x-AB)2,
整理,得x2-2ABx=4,
同理,得(AB-0.5)2+32=(x-AB+0.5)2,
整理,得x2-2ABx+x=9,
解得x=5.
∴原来标杆的高度为5米.
设原标杆的高为x,
∵∠A=90°,
∴由题中条件可得AB2+AC2=BC2,即AB2+22=(x-AB)2,
整理,得x2-2ABx=4,
同理,得(AB-0.5)2+32=(x-AB+0.5)2,
整理,得x2-2ABx+x=9,
解得x=5.
∴原来标杆的高度为5米.
点评:本题主要考查了简单的勾股定理的应用问题,能够熟练掌握.

练习册系列答案
相关题目
下列图形中,是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |

 如图,已知F、G是OA上两点,M、N是OB上两点,且FG=MN,S△PFG=S△PMN,试问:点P是否在∠AOB的平分线上?
如图,已知F、G是OA上两点,M、N是OB上两点,且FG=MN,S△PFG=S△PMN,试问:点P是否在∠AOB的平分线上?