题目内容
若x3+x2+x+1=0,则1+x+x2+x3+…+x99的值是 .
考点:因式分解的应用
专题:
分析:由条件的x3+x2+x+1=0可以推断得到(x3+x2)+(x+1)=x2(x+1)+(x+1)=(x2+1)(x+1)=0,所以可以推导得到x=-1,代入代数式即可求解.
解答:解:∵x3+x2+x+1=0,
∴(x3+x2)+(x+1)=x2(x+1)+(x+1)=(x2+1)(x+1)=0,
∴x+1=0,
解得:x=-1,
∴1+x+x2+x3+…+x99=1+(-1)+(-1)2+(-1)3+…+(-1)99═1-1+1-1+1-1…-1=0,
故答案为:0.
∴(x3+x2)+(x+1)=x2(x+1)+(x+1)=(x2+1)(x+1)=0,
∴x+1=0,
解得:x=-1,
∴1+x+x2+x3+…+x99=1+(-1)+(-1)2+(-1)3+…+(-1)99═1-1+1-1+1-1…-1=0,
故答案为:0.
点评:本题考查了因式分解的应用,解题的关键是能正确的通过因式分解求得x的值,难度不大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
一个学习小组利用同一块木板,测量了小车从不同高度下滑的时间,他们得到如下数据:
下列说法错误的是( )
| 支撑物高度h(cm) | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
| 小车下滑时间t(s) | 4.23 | 3.00 | 2.45 | 2.13 | 1.89 | 1.71 | 1.59 | 1.50 |
| A、当h=50cm时,t=1.89s |
| B、随着h逐渐升高,t逐渐变小 |
| C、h每增加10cm,t减小1.23s |
| D、随着h逐渐升高,小车的速度逐渐加快 |
 如图称为“trefoil”,作法是在彼此完全相同的等边三角形的边上画圆弧.如图中水平的底边长度为2,则整个图形的面积为
如图称为“trefoil”,作法是在彼此完全相同的等边三角形的边上画圆弧.如图中水平的底边长度为2,则整个图形的面积为
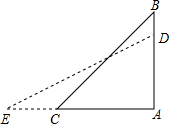 如图,有一直立标杆,它的上部被风从B处吹折,杆顶C着地,离杆脚2m,修好后又被风吹折,因新断处D比前一次低0.5m,故杆顶E着地比前次远1m,求原标杆的高度.
如图,有一直立标杆,它的上部被风从B处吹折,杆顶C着地,离杆脚2m,修好后又被风吹折,因新断处D比前一次低0.5m,故杆顶E着地比前次远1m,求原标杆的高度.