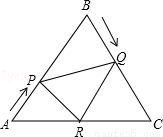
题目内容
下列命题中，正确的是（ ）
①顶点在圆周上的角是圆周角；②圆周角的度数等于圆心角度数的一半；③90°的圆周角所对的弦是直径；④不在同一条直线上的三个点确定一个圆；⑤同弧所对的圆周角相等
A．①②③ B．③④⑤ C．①②⑤ D．②④⑤
B.
【解析】
试题分析：根据圆周角定理及推论，分别进行判定即可．
解答：【解析】
根据圆周角定理可知：①顶点在圆周上且两边与圆相交的角是圆周角，故此选项错误；
②圆周角的度数等于圆心角度数的一半；根据同弧或等弧所对圆周角等于圆心角的一半，故此选项错误；
③90°的圆周角所对的弦是直径；根据圆周角定理推论可知，此选项正确；
④不在同一条直线上的三个点确定一个圆； 根据不在一条直线上的三点可确定一个圆，故此选项正确；
⑤同弧所对的圆周角相等，∵在同圆或等圆中，同弧所对的圆周角相等，故此选项正确；
所以③④⑤正确．
故选B.
考点：1.圆周角定理；2.确定圆的条件；3.命题与定理．
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
（本题12分）为鼓励居民节约用电，某地试行阶梯电价收费制，具体执行方案如表：
档次 | 每户每月用电数（度） | 执行电价（元/度） |
第一档 | 小于等于200部分 | 0.5 |
第二档 | 大于200小于400部分 | 0.6 |
第三档 | 大于等于400部分 | 0.8 |
（1）该地一户居民四月份用电180度，则需缴电费多少元？
（2）某居民八月份用电
度（
＞400），用的代数式表示该户八月份需交电费多少元？
（3）又一户居民五、六月份共用电500度，缴电费262元．已知该用户六月份用电量大于五月份，且五六月份的用电量均小于400度．问该户居民五、六月份各月用电多少度？
）,（-1,
）,（3,
）是二次函数
上的点,则
的大小关系（）
B. 
C. 
D. 
－（4k+1)x+3k+3=0．
