题目内容
16.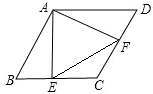 在菱形ABCD中,E、F分别是BC、CD的中点,连结AE、AF.
在菱形ABCD中,E、F分别是BC、CD的中点,连结AE、AF.求证:AE=AF.
分析 根据菱形的性质可以得出AB=BC=CD=AD,∠B=∠D,进而就可以得出△ABE≌△ADF,从而得出AE=AF.
解答 证明:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,∠B=∠D,
∴$\frac{1}{2}$BC=$\frac{1}{2}$CD.
∵E、F分别是BC、CD的中点,
∴BE=$\frac{1}{2}$BC,DF=$\frac{1}{2}$CD,
∴BE=DF.
在△ABE和△ADF中
$\left\{\begin{array}{l}{AB=AD}\\{∠B=∠D}\\{BE=DF}\end{array}\right.$,
∴△ABE≌△ADF(SAS),
∴AE=AF.
点评 本题考查了菱形的性质的运用,线段的中点的性质的运用,全等三角形的判定及性质的运用,解答时运用菱形的性质证明三角形全等是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.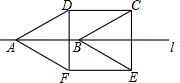 如图,将边长为2cm的菱形ABCD沿边AB所在的直线l翻折180°得到四边形ABEF,若∠DAB=30°,则四边形CDEF的面积为( )
如图,将边长为2cm的菱形ABCD沿边AB所在的直线l翻折180°得到四边形ABEF,若∠DAB=30°,则四边形CDEF的面积为( )
 如图,将边长为2cm的菱形ABCD沿边AB所在的直线l翻折180°得到四边形ABEF,若∠DAB=30°,则四边形CDEF的面积为( )
如图,将边长为2cm的菱形ABCD沿边AB所在的直线l翻折180°得到四边形ABEF,若∠DAB=30°,则四边形CDEF的面积为( )| A. | 2cm2 | B. | 3cm2 | C. | 4cm2 | D. | 6cm2 |
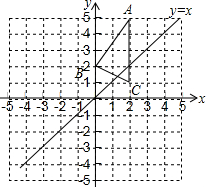 △ABC在平面直角坐标系中的位置如图所示,A、B、C三点的坐标分别为(2,5)、(0,2)、(2,1).
△ABC在平面直角坐标系中的位置如图所示,A、B、C三点的坐标分别为(2,5)、(0,2)、(2,1). 如图:AD∥BC,∠DAC=60°,∠ACF=25°,∠EFC=145°,∠B=54°,则∠BEF=126°.
如图:AD∥BC,∠DAC=60°,∠ACF=25°,∠EFC=145°,∠B=54°,则∠BEF=126°.