题目内容
4.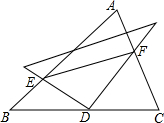 如图,点D是△ABC的边BC中点,将一把直角三角尺的直角顶点放于D处,其两条直角边分别交AB、AC于点E、F.试比较BE+CF与EF的大小,并说明理由.
如图,点D是△ABC的边BC中点,将一把直角三角尺的直角顶点放于D处,其两条直角边分别交AB、AC于点E、F.试比较BE+CF与EF的大小,并说明理由.
分析 先利用ASA判定△BGD≌△CFD,从而得出BG=CF,GD=FD,再有DE⊥GF,从而得出EG=EF,两边和大于第三边从而得出BE+CF>EF.
解答 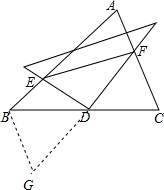 解:BE+CF>EF.
解:BE+CF>EF.
理由:作BG∥AC,交FD的延长线于G,
∴∠DBG=∠DCF.
∵D为BC的中点,
∴BD=CD
又∵∠BDG=∠CDF,
在△BGD与△CFD中,
$\left\{\begin{array}{l}{∠DBG=∠DCF}\\{BD=CD}\\{∠BDG=∠CDF}\end{array}\right.$
∴△BGD≌△CFD(ASA).
∴GD=FD,BG=CF.
又∵DE⊥FG,
∴EG=EF(垂直平分线到线段端点的距离相等).
∴在△EBG中,BE+BG>EG,
即BE+CF>EF.
点评 本题考查全等三角形的判定和性质以及三角形三边关系,判定两个三角形全等的一般方法有:SSS、SAS、AAS、ASA、HL.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
19.|a|+a=2a,则a是( )
| A. | 0 | B. | 负数 | C. | 非负数 | D. | 正数 |
16.下列调查中,最适宜采取普查的( )
| A. | 一批洗衣机的使用寿命 | |
| B. | 了解某市中学生课外阅读的情况 | |
| C. | 《新闻联播》电视栏目的收视率 | |
| D. | 调查乘坐飞机的旅客是否携带了危禁物品 |
14.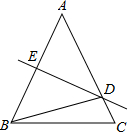 如图,在△ABC中,AB=AC,AB的垂直平分线DE交AC于D,交AB于E,∠DBC=15°,则∠A的度数是( )
如图,在△ABC中,AB=AC,AB的垂直平分线DE交AC于D,交AB于E,∠DBC=15°,则∠A的度数是( )
 如图,在△ABC中,AB=AC,AB的垂直平分线DE交AC于D,交AB于E,∠DBC=15°,则∠A的度数是( )
如图,在△ABC中,AB=AC,AB的垂直平分线DE交AC于D,交AB于E,∠DBC=15°,则∠A的度数是( )| A. | 50° | B. | 20° | C. | 30° | D. | 25° |
 如图,在△ABC中,AB=AC,∠BAC=120°.
如图,在△ABC中,AB=AC,∠BAC=120°.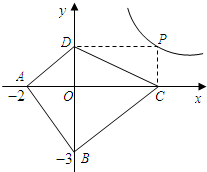 阅读理解:对于任意正实数a、b,∵$(\sqrt{a}-\sqrt{b})^{2}$≥0,∴$a-2\sqrt{ab}+b$≥0,∴a+b≥$2\sqrt{ab}$只有当a=b时,等号成立.
阅读理解:对于任意正实数a、b,∵$(\sqrt{a}-\sqrt{b})^{2}$≥0,∴$a-2\sqrt{ab}+b$≥0,∴a+b≥$2\sqrt{ab}$只有当a=b时,等号成立.