Question

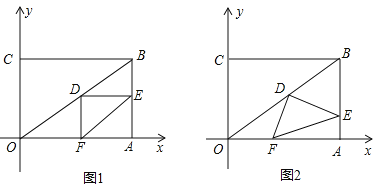
【题目】矩形AOBC中，OB＝4，OA＝3，分别以OB，OA所在直线为x轴，y轴，建立如图所示的平面直角坐标系，F是BC边上一个动点（不与B，C重合），过点F的反比例函数（k＞0）的图象与边AC交于点E．

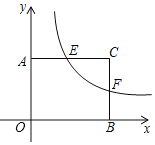
（1）当点F为边BC的中点时，求点E的坐标；（2）连接EF，求∠EFC的正切值．

Answer 1

【答案】（1）E（2，3）；（2）tan∠EFC=.

【解析】

（1）求出B（4，0），C（4，3），F（4，），用待定系数法求函数解析式，再求E坐标；（2）根据函数解析式，求出E,F坐标，得到CF=BC﹣BF=3﹣=，CE=AC﹣AE=4﹣=可进一步求出∠EFC的正切值=.

解：（1）∵OA=3，OB=4，

∴B（4，0），C（4，3），

∵F是BC的中点，

∴F（4，），

∵F在反比例y=函数图象上，

∴k=4×=6，

∴反比例函数的解析式为y=

∵E点的纵坐标为3，

∴E（2，3）；

（2）∵F点的横坐标为4，且在y=上，

∴F（4，），

∴CF=BC﹣BF=3﹣=

∵E的纵坐标为3，且在y=上，

∴E（，3），

∴CE=AC﹣AE=4﹣=，

在Rt△CEF中，tan∠EFC=.