题目内容
知识背景:火晶柿子是我市临潼区特有的柿树品种,因其个小色红,晶莹光亮,皮薄无核深受国内外游客欢迎.在市场出售时,要求“火晶柿子”用双层上盖的长方体纸箱封装(上盖纸板面积刚好等于底面积的2倍,如图)
(1)实际运用:如果要求纸箱的高位0.5米,底面是黄金矩形(宽与长的黄金比,取黄金比为0.6),体积为0.3立方米.为制作纸箱,小明设计两种方案,如下图:
①若按方案1做一个纸箱,需要矩形硬纸板A1B1C1D1的面积是 平方米;
②如果从节省材料的角度考虑,你会选择方案 ,并说明理由.(方案2)是用菱形硬纸板A2B2C2D2做一个纸箱)
(2)拓展思维:一家水果商打算在临潼购进一批“火晶柿子”但他感觉(1)中的纸箱体积太大,搬运吃力,要求将纸箱的底面周长、底面积和高度设计为原来的一般,你认为水果商的要求能办到吗?如果能,请帮他算出纸箱的尺寸;如果不能,请说明理由.
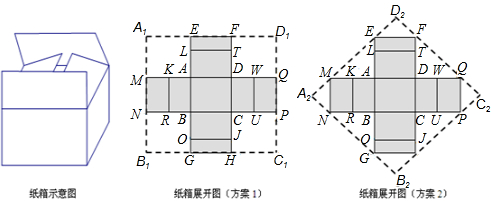
(1)实际运用:如果要求纸箱的高位0.5米,底面是黄金矩形(宽与长的黄金比,取黄金比为0.6),体积为0.3立方米.为制作纸箱,小明设计两种方案,如下图:
①若按方案1做一个纸箱,需要矩形硬纸板A1B1C1D1的面积是
②如果从节省材料的角度考虑,你会选择方案
(2)拓展思维:一家水果商打算在临潼购进一批“火晶柿子”但他感觉(1)中的纸箱体积太大,搬运吃力,要求将纸箱的底面周长、底面积和高度设计为原来的一般,你认为水果商的要求能办到吗?如果能,请帮他算出纸箱的尺寸;如果不能,请说明理由.

考点:相似三角形的应用,菱形的性质,矩形的性质
专题:
分析:(1)①利用宽与长的比是黄金比,取黄金比为0.6,假设底面长为x,宽就为0.6x,再利用图形得出QM=
+0.5+1+0.5+
=3,FH=0.3+0.5+0.6+0.5+0.3=2.2,进而求出即可;
②根据菱形的性质得出,对角线乘积的一半绝对小于矩形边长乘积即可得出答案;
(2)根据相似三角形的性质面积比等于相似比的平方得出即可.
| 1 |
| 2 |
| 1 |
| 2 |
②根据菱形的性质得出,对角线乘积的一半绝对小于矩形边长乘积即可得出答案;
(2)根据相似三角形的性质面积比等于相似比的平方得出即可.
解答:解:(1)①∵纸箱的高为0.5米,底面是黄金矩形(宽与长的比是黄金比,取黄金比为0.6),体积为0.3立方米,
∴假设底面长为x,宽就为0.6x,
∴体积为:0.6x•x•0.5=0.3,
解得:x=1,
∴AD=1,CD=0.6,
DW=KA=DT=JC=0.5,FT=JH=CD=0.3,
WQ=MK=
AD=
,
∴QM=
+0.5+1+0.5+
=3,
FH=0.3+0.5+0.6+0.5+0.3=2.2,
∴矩形硬纸板A1B1C1D1的面积是3×2.2=6.6平方米;
②从节省材料的角度考虑,采用方案2(如图)的菱形硬纸板A2B2C2D2做一个纸箱比方案1更优,
∵如图可知△MAE,△NBG,△HCF,△FDQ面积相等,且和为2个矩形FDQD1,
又∵菱形的性质得出,对角线分别等于矩形的长与宽的菱形的面积小于矩形的面积;
∴从节省材料的角度考虑,采用方案2(如图)的菱形硬纸板A2B2C2D2做一个纸箱比方案1更优,
(2)∵将纸箱的底面周长、底面面积和高都设计为原来的一半时,
∴边长为:0.5,0.3,底面积将变为:0.3×0.5=0.15,
将变为原来的
,高再变为原来的一半时,体积将变为原来的
,
∴水果商的要求不能办到.
∴假设底面长为x,宽就为0.6x,
∴体积为:0.6x•x•0.5=0.3,
解得:x=1,
∴AD=1,CD=0.6,
DW=KA=DT=JC=0.5,FT=JH=CD=0.3,
WQ=MK=
| 1 |
| 2 |
| 1 |
| 2 |
∴QM=
| 1 |
| 2 |
| 1 |
| 2 |
FH=0.3+0.5+0.6+0.5+0.3=2.2,
∴矩形硬纸板A1B1C1D1的面积是3×2.2=6.6平方米;
②从节省材料的角度考虑,采用方案2(如图)的菱形硬纸板A2B2C2D2做一个纸箱比方案1更优,
∵如图可知△MAE,△NBG,△HCF,△FDQ面积相等,且和为2个矩形FDQD1,
又∵菱形的性质得出,对角线分别等于矩形的长与宽的菱形的面积小于矩形的面积;
∴从节省材料的角度考虑,采用方案2(如图)的菱形硬纸板A2B2C2D2做一个纸箱比方案1更优,
(2)∵将纸箱的底面周长、底面面积和高都设计为原来的一半时,
∴边长为:0.5,0.3,底面积将变为:0.3×0.5=0.15,
将变为原来的
| 1 |
| 4 |
| 1 |
| 8 |
∴水果商的要求不能办到.
点评:此题主要考查了一元二次方程的应用以及正方形性质与菱形性质等知识,根据题意得出DW=KA=DT=JC=0.5,FT=JH=12CD=0.3,WQ=MK=12AD=12是解决问题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
已知有理式:
,
,
,
,
x2,
+4,其中分式有( )
| 4 |
| x |
| a+b |
| π |
| 1 |
| x-y |
| 3x |
| 4 |
| 1 |
| 2 |
| 1 |
| a |
| A、2个 | B、3个 | C、4个 | D、5个 |
在平面直角坐标系中,第二象限内有一点P,且点P到x轴的距离是4,到原点的距离是5,则P点坐标是( )
| A、(-5,4) |
| B、(-3,5) |
| C、(-4,3) |
| D、(-3,4) |
若关于x的一元一次不等式组
无解,则m的取值范围为( )
|
A、m≤
| ||
B、m>
| ||
C、m>-
| ||
D、m≤-
|
截止6月10日,上海世博会累计入园人数已达1231.54万.将1231.54万人用科学记数法(四舍五入保留3个有效数字)表示约为( )
| A、12.3×106人 |
| B、1.23×107人 |
| C、1.23×106人 |
| D、0.123×108人 |
 如图,把等边△ABC的外接圆对折,使点A的劣弧BC的中点M重合,折痕分别交AB、AC于D、E,若BC=6,则线段DE的长为
如图,把等边△ABC的外接圆对折,使点A的劣弧BC的中点M重合,折痕分别交AB、AC于D、E,若BC=6,则线段DE的长为 计算变压器铁芯片阴影部分的面积为
计算变压器铁芯片阴影部分的面积为