Question

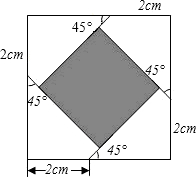现有若干张边长不相等但都大于4cm的正方形纸片，从中任选一张，如图从距离正方形的四个顶点2cm处，沿45°角画线，将正方形纸片分成5部分，则中间阴影部分的面积是

 

cm²；若在上述正方形纸片中再任选一张重复上述过程，并计算阴影部分的面积，你能发现什么规律？

Answer 1

分析：延长小正方形的一边交大正方形于一点，连接此点与距大正方形顶点2cm处的点，构造直角边长为2的等腰直角三角形，将小正方形的边长转化为等腰直角三角形的斜边长来求解即可．

解答：解：如图，延长小正方形的一边AB，与大正方形的一边交于C点，连接CD，
∴△CED为直角边长为2cm的等腰直角三角形，
∴CD=

2

DE=2

2

，
∴阴影正方形的边长=AB=2

2

cm，
∴阴影正方形的面积为：8cm²；

规律：现有若干张边长不相等但都大于2acm的正方形纸片，从中任选一张，从距离正方形的四个顶点acm处，沿45°角画线，将正方形纸片分成5部分，则中间阴影部分的面积是2a²cm²．
故答案为：8．

点评：本题考查了正方形的性质，勾股定理及学生的逻辑思维能力，题目同时也渗透了转化思想．