题目内容
有下列说法:
①若ac<0,则方程cx2+bx+a=0有两个不相等的实数根;
②若b=2a+
c,则一元二次方程ax2+bx+c=0必有一根为-2;
③若b2-4ac=0,则方程cx2+bx+a=0有两个相等的实数根.
其中错误的个数是( )
①若ac<0,则方程cx2+bx+a=0有两个不相等的实数根;
②若b=2a+
| 1 |
| 2 |
③若b2-4ac=0,则方程cx2+bx+a=0有两个相等的实数根.
其中错误的个数是( )
| A、0 | B、1 | C、2 | D、3 |
考点:根的判别式,一元二次方程的解
专题:
分析:根据ac<0得到△=b2-4ac>0,于是可根据判别式的意义对①进行判断;由于b=2a+
c可变形为4a-2b+c=0,于是根据一元二次方程的解的定义对②进行判断;先进行讨论得到c≠0,则可根据判别式的意义对③进行判断.
| 1 |
| 2 |
解答:解:若ac<0,则△=b2-4ac>0,方程cx2+bx+a=0有两个不相等的实数根,所以①的说法正确;若b=2a+
c,则4a-2b+c=0,所以一元二次方程ax2+bx+c=0必有一根为-2,所以②的说法正确;若b2-4ac=0,由于c=0时,b=0,原等式不是方程,即c≠0,所以方程cx2+bx+a=0有两个相等的实数根,所以③的说法正确.
故选A.
| 1 |
| 2 |
故选A.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了一元二次方程的解.

练习册系列答案
相关题目
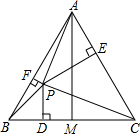 如图,P是等边△ABC内任意一点,由P向边BC、AC、AB分别引垂线段PD、PE、PF,AM⊥BC,AM=6cm,则PD+PE+PF=
如图,P是等边△ABC内任意一点,由P向边BC、AC、AB分别引垂线段PD、PE、PF,AM⊥BC,AM=6cm,则PD+PE+PF= 今年“十一”黄金周期间,某风景区在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数,单位:万人):
今年“十一”黄金周期间,某风景区在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数,单位:万人):