Question

8．如图放置的△OAB₁，△B₁A₁B₂，△B₂A₂B₃，…都是边长为2的等边三角形，边AO在y轴上，点B₁，B₂，B₃，…都在直线y=$\frac{\sqrt{3}}{3}$x上，则B₂₀₁₆的坐标是（2016$\sqrt{3}$，2016）．

Answer 1

分析 过B₁作B₁C⊥x轴，垂足为C，由条件可求得∠B₁OC=30°，利用直角三角形的性质可求得B₁C=1，OC=$\sqrt{3}$，可求得B₁的坐标，同理可求得B₂、B₃的坐标，则可得出规律，可求得B₂₀₁₆的坐标．

解答 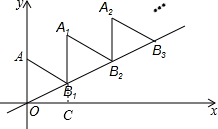解：
如图，过B₁作B₁C⊥x轴，垂足为C，
∵△OAB₁是等边三角形，且边长为2，
∴∠AOB₁=60°，OB₁=2，
∴∠B₁OC=30°，
在RtB₁OC中，可得B₁C=1，OC=$\sqrt{3}$，
∴B₁的坐标为（$\sqrt{3}$，1），
同理B₂（2$\sqrt{3}$，2）、B₃（3$\sqrt{3}$，3），
∴B_n的坐标为（n$\sqrt{3}$，n），
∴B₂₀₁₆的坐标为（2016$\sqrt{3}$，2016），
故答案为：（2016$\sqrt{3}$，2016）．

点评 本题为规律型题目，利用等边三角形和直角三角形的性质求得B₁的坐标，从而总结出点的坐标的规律是解题的关键．