Question

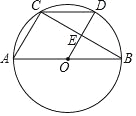
【题目】在△AOB中，C，D分别是OA、OB边上的点，将△OCD绕点O顺时针旋转到△OC′D′．如图，若∠AOB=90°，OA=OB，C，D分别为OA，OB的中点．求证：

(1)AC′=BD′；

(2)AC′⊥BD．

Answer 1

【答案】（1）证明见解析；（2）证明见解析.

【解析】

(1)由旋转的性质得出OC=OC′，OD=OD′，∠AOC′=∠BOD′，证出OC′=OD′，由SAS证明△AOC′≌△BOD′，得出对应边相等即可；

(2)由全等三角形的性质得出∠OAC′=∠OBD′，又由对顶角相等和三角形内角和定理得出∠BEA=90°，即可得出结论

（1）∵将△OCD绕点O顺时针旋转到△，

∴OC=，OD=，∠=∠．

∵OA=OB，C、D为OA，OB的中点，

∴OC=OD，

∴．

在△和△中，，

∴△≌△，

∴=．

（2）延长交于E，交BO于F．

∵△≌△，

∴∠．

又∠AFO=∠BFE，∠，

∴∠．

∴∠BEA=，

∴⊥．