Question

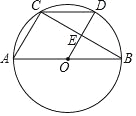
【题目】如图，AB是⊙O的直径，弦BC垂直且平分半径OD，AB＝6，

(1)求∠ABC的度数；

(2)求BC的长．

Answer 1

【答案】（1）∠ABC＝30°；（2）BC＝3．

【解析】

（1）通过连接BD，因为弦BC垂直且平分半径OD，可得BO＝BD，又因为BO=OD（都是半径），可知BO＝BD=OD，则△ODB是等边三角形，得到∠ABD＝60°，再利用等腰三角形三线合一，即可求出∠ABC度数.

（2）AB是直径，可知△ACB是直角三角形，解这个直角三角形即可得到答案.

解：（1）如图连接BD．

∵BC垂直平分线段OD，

∴BO＝BD，

∵OD＝OB，

∴OD＝OB＝BD，

∴△ODB是等边三角形，

∴∠ABD＝60°，

∵BE⊥OD，

∴∠ABC＝∠OBD＝30°，

（2）

∵AB是直径，

∴∠ACB＝90°，

∵AB＝6，∠ABC＝30°，

∴BC＝ABcos30°＝3．