题目内容
如果两个二次函数图象的开口向上,顶点坐标都相同,那么称这两个二次函数互为“同簇二次函数”,显然“同簇二次函数”不是唯一的.
(1)已知二次函数y=3x2﹣6x+1.
①写出它的开口方向,顶点坐标;
②请写出它的两个不同的“同簇二次函数”.
(2)已知两个二次函数y1=a1(x﹣k1)2+h1,y2=a2(x﹣k2)2+h2是“同簇二次函数”,则a1a2 0,k1 k2,h1 h2(均填“>”、“=“、或“<”号)
①如果y3=y1+y2也是y1的“同簇二次函数”,求证:y3的顶点在x轴上;
②如果直线y=t,与y1、y2顺次交于点A、B、C、D,且AB=BC=CD,求
 的值.
的值.
【考点】二次函数综合题.
【分析】(1)①由a>0,可判断出抛物线的开口方向,然后利用配方法可求得抛物线的顶点坐标;
②由“同簇二次函数”的定义写出两个顶点坐标为(1,﹣2),a≠3的二次函数即可;
(2)由同簇二次函数可知a1>0,a2>0,k1=k2,h1=h2;
①列出关于y3的函数关系式,然后依据“同簇二次函数”的定义可求得h1=0,从而可求得y3的顶点在x轴上;
②分别求得y1=a1(x﹣k1)2+h1与y=t、y2=a2(x﹣k1)2+h1与y=t的交点横坐标,最后依据AD=3BC可求得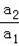
 的值.
的值.
【解答】解:(1)①∵a=3>0,
∴抛物线的开口向上.
∵y=3x2﹣6x+1=3(x﹣1)2﹣2,
∴抛物线的顶点坐标为(1,﹣2).
②由“同簇二次函数”的定义可知y1=2(x﹣1)2﹣2,y2=(x﹣1)2﹣2均是y=3x2﹣6x+1的同簇二次函数.
(2)∵由同簇二次函数可知a1>0,a2>0,k1=k2,h1=h2,
∴a1a2>0,k1=k2,h1=h2.
故答案为:>,=,=.
①∵y3=y1+y2,
∴y3=a1(x﹣k1)2+h1+a2(x﹣k2)2+h2.
∵k1=k2,h1=h2,
∴y3=(a1+a2)(x﹣k1)2+2h1.
∵y3与y1互为同簇二次函数.
∴2h1=h1.
解得h1=0.
∴y3=(a1+a2)(x﹣k1)2.
∴y3的顶点在x轴上.
②将y1=a1(x﹣k1)2+h1与y=t联立解得:x=k1±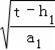
 .
.
将y2=a2(x﹣k1)2+h1与y=t联立解得:x=k1±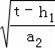
 .
.
∵AB=BC=CD,
∴AD=3BC.
∴2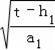
 =6
=6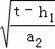
 .
.
解得: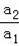
 =9.
=9.
【点评】本题主要考查的是二次函数的综合应用,解答本题主要应用了配方法求二次函数的顶点坐标、函数图象的交点与方程组的关系、理解同簇二次函数的概念是解题的关键.

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案某居民小区开 展节约用电活动,对该
展节约用电活动,对该 小区100户家庭的节电量情况进行了统计, 4月份与3月份相比,节电情况如下表:
小区100户家庭的节电量情况进行了统计, 4月份与3月份相比,节电情况如下表:
| 节电量(千瓦时) |
| 30 | 40 | 50 |
| 户 数 | 10 | 40 | 30 | 20 |
则4月份这100户节电量的平均数、中位数、众数分别是( )
A. 35、35、30 B. 25、30、20 C. 36、35、30 D. 36、30、30
 经过点A(3,8)和B(
经过点A(3,8)和B( ,
, ).
). 时,y的值.
时,y的值. 20
20



 稳定.
稳定.